Consider the following Horn clauses in first-order logic. 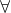x,y [Start(x,y) & Unpopular(y) => Unpopular(x)] 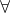z,e [Unpopular(z) & Candidate(z,e) => Lose(z,e)] 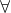s,u,w [Candidate(u,s) & Candidate(w,s) & w!=u & Lose(u,s) => Win(w,s)] Candidate(Barack, Election) Candidate(George, Election) Start(George, IraqWar) Unpopular(IraqWar)

Use backward-chaining rule-based inference to answer the query: Win(v,Election). Show the trace of the search conducted and the subgoals generated and show the final answer retrieved. Assume that the operator "!=" (not equal) is evaluated procedurally (i.e. handled externally by a special program that returns the correct truth value).

Transcribed image text