Consider the following linear programming problem:

Max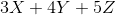

s.t.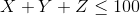

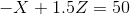
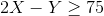
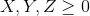
Part A: Put the problem into standard form (a maximization subject only to less than or equal to constraints) and clearly identify dual variables with each of the constraints in the standard form of the problem. Let the dual variables be 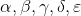and so on, using as many lowercase Greek letters as needed so that you have one dual variable for each of the primal constraints in the problem in standard form.

Part B: Write out the dual of the problem in terms of the notation used in Part A.

Part C: The optimal solution to this problem is given by, 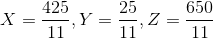and the optimal primal objective function value is given by 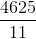. If the dual variable associated with the first constraints is 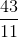, what will the objective function value be if we increase the right hand side of the constraint to 125? (the Sensitivity Analysis report for this problem shows that this increase of 25 is well within the allowable limit on the increase for this constant.)

2X - Y > 75 Y, Z 2X - Y > 75 Y, Z