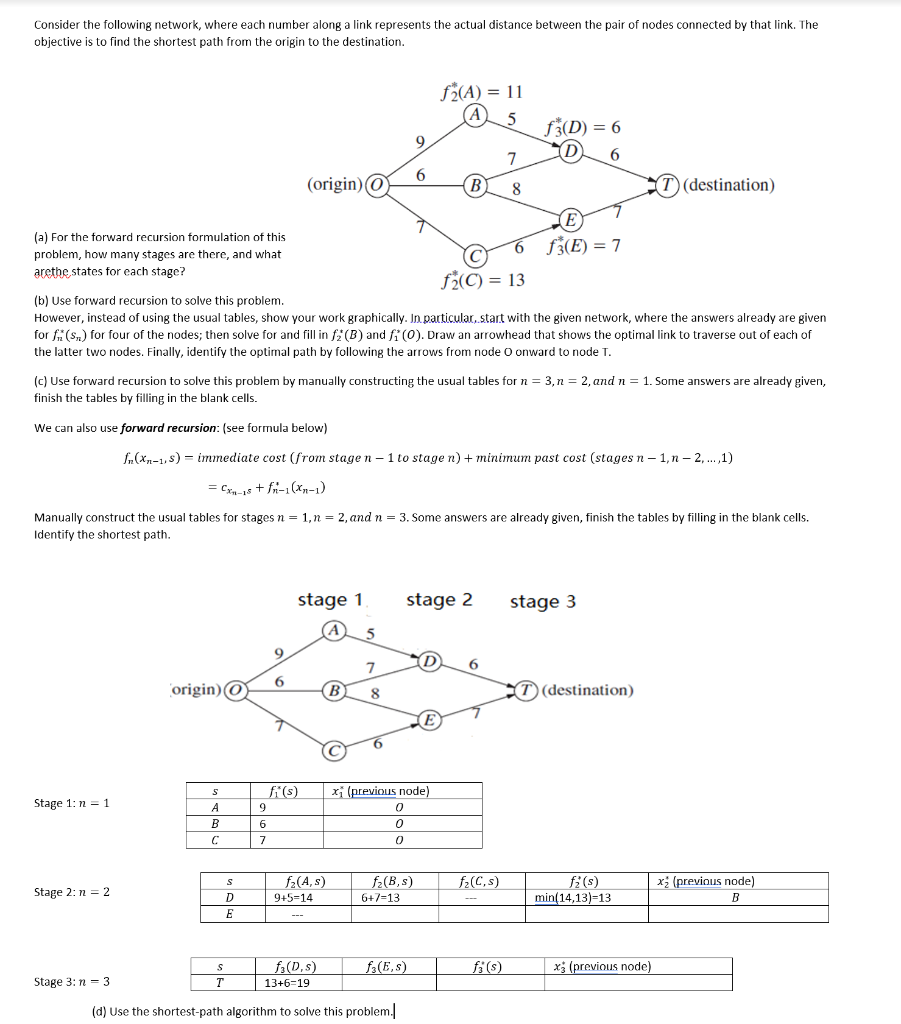
Consider the following network, where each number along a link represents the actual distance between the pair of nodes connected by that link. The objective is to find the shortest path from the origin to the destination. (a) For the forward recursion formulation of this problem, how many stages are there, and what arethestates for each stage? (b) Use forward recursion to solve this problem. However, instead of using the usual tables, show your work graphically. In particular, start. with the given network, where the answers already are given for fn(sn) for four of the nodes; then solve for and fill in f2(B) and f1(O). Draw an arrowhead that shows the optimal link to traverse out of each of the latter two nodes. Finally, identify the optimal path by following the arrows from node O onward to node T. (c) Use forward recursion to solve this problem by manually constructing the usual tables for n=3,n=2, and n=1. Some answers are already given, finish the tables by filling in the blank cells. We can also use forward recursion: (see formula below) fn(xn1,s)=immediatecost(ffomstagen1tostagen)+minimumpastcost(stagesn1,n2,,1)=cxn1s+fn1(xn1) Manually construct the usual tables for stages n=1,n=2, and n=3. Some answers are already given, finish the tables by filling in the blank cells. Identify the shortest path. Stage 1: n=1 Stage 2:n=2 Stage 3:n=3 (d) Use the shortest-path algorithm to solve this problem.| Consider the following network, where each number along a link represents the actual distance between the pair of nodes connected by that link. The objective is to find the shortest path from the origin to the destination. (a) For the forward recursion formulation of this problem, how many stages are there, and what arethestates for each stage? (b) Use forward recursion to solve this problem. However, instead of using the usual tables, show your work graphically. In particular, start. with the given network, where the answers already are given for fn(sn) for four of the nodes; then solve for and fill in f2(B) and f1(O). Draw an arrowhead that shows the optimal link to traverse out of each of the latter two nodes. Finally, identify the optimal path by following the arrows from node O onward to node T. (c) Use forward recursion to solve this problem by manually constructing the usual tables for n=3,n=2, and n=1. Some answers are already given, finish the tables by filling in the blank cells. We can also use forward recursion: (see formula below) fn(xn1,s)=immediatecost(ffomstagen1tostagen)+minimumpastcost(stagesn1,n2,,1)=cxn1s+fn1(xn1) Manually construct the usual tables for stages n=1,n=2, and n=3. Some answers are already given, finish the tables by filling in the blank cells. Identify the shortest path. Stage 1: n=1 Stage 2:n=2 Stage 3:n=3 (d) Use the shortest-path algorithm to solve this problem.|