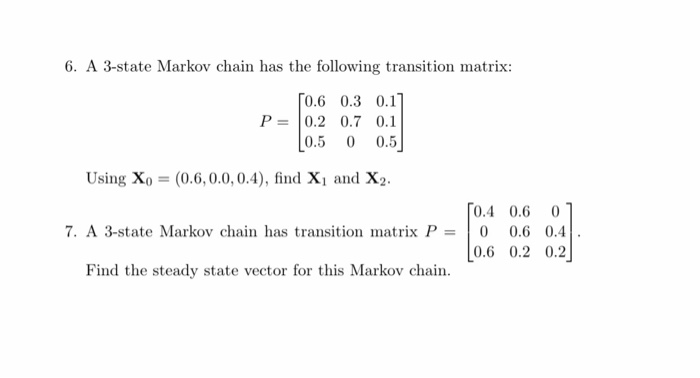
Question
Consider the following OCV-SOC model: V0(s) = k0 + k1s + k2s 1 + k3s 2 + k4s 3 + k5s 4 + k6 ln(s)


Consider the following OCV-SOC model: V0(s) = k0 + k1s + k2s 1 + k3s 2 + k4s 3 + k5s 4 + k6 ln(s) + k7 ln(1 s) (1) where k0 = 9.082, k1 = 76.604, k2 = 103.087, k3 = 18.185, k4 = 2.062, k5 = 0.102, k6 = 141.199, and k7 = 1.117. These parameters were computed for SOC values s [0, 1] after they were linearly scaled to s 0 [.175, .825].
find the SOC of the given battery corresponding to a measure OCV of 3.75 V. Assume that there is voltage measurement error and we need to find out the resulting SOC error. It is given that the voltage measurement error is zero-mean with standard deviation 10 mV.
(a) Use the following Monte-Carlo simulation approach to find out the standard deviation of the error in SOC error
- Generate 1000 'voltage measurements' using the above-mentioned measurement error (zero-mean, standard deviation of 10 mV). The Matlab command '3.75 + 0.01*randn(1000,1)' will generate these 1000 measurements. The standard deviation of these measurements is 0.01 V (or 10 mV). - Compute the SOC corresponding to each of these 1000 voltage measurements
- Compute the SOC corresponding to OCV = 3.75 V
- Compute the SOC computation error corresponding to each of the 1000 measurements
- Compute the standard deviation of the SOC computation error
(b) Repeat the above for SOC estimation corresponding to an OCV of 3.95 V
(c) Repeat the above for SOC estimation corresponding to an OCV of 3.6 V
(d) Repeat the above for SOC estimation corresponding to an OCV of 3.3 V
(e) Consider the following statement: "Given the same voltage measurement, the error in computed SOC varies depending on the SOC region" Do you agree or disagree with the above statement? justify your answer.




Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


