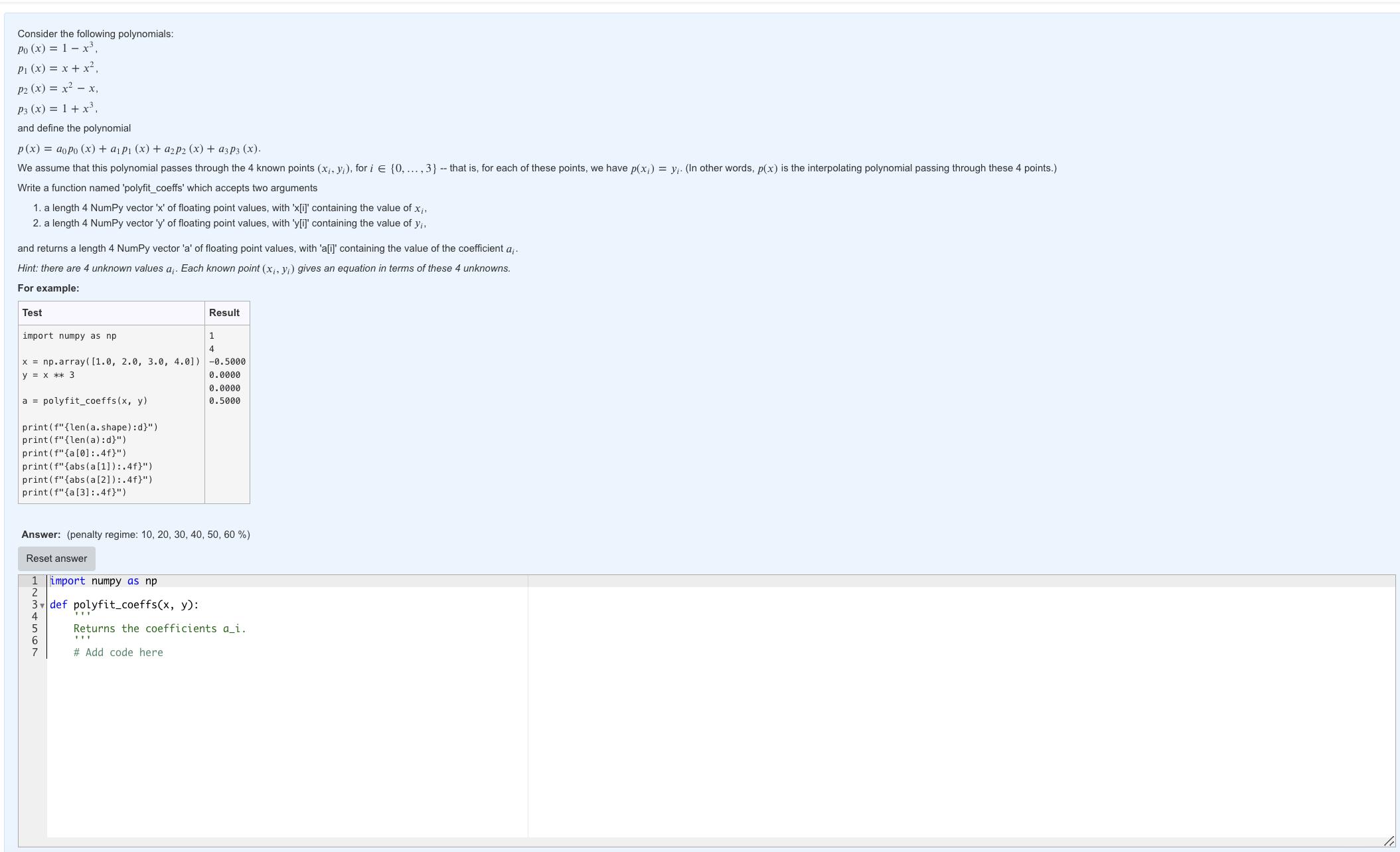
Consider the following polynomials: Po (x) = 1- x, P (x) = x + x, P2 (x) = x - x, P3 (x) = 1 + x, and define the polynomial p(x) = aopo (x) + ap (x) + a2P2 (x) + a3p3 (x). We assume that this polynomial passes through the 4 known points (x, y), for i E {0,..., 3} -- that is, for each of these points, we have p(x) = y. (In other words, p(x) is the interpolating polynomial passing through these 4 points.) Write a function named 'polyfit_coeffs' which accepts two arguments 1. a length 4 NumPy vector 'x' of floating point values, with 'x[i]' containing the value of x, 2. a length 4 NumPy vector 'y' of floating point values, with 'y[i]' containing the value of yi, and returns a length 4 NumPy vector 'a' of floating point values, with 'a[i]' containing the value of the coefficient a. Hint: there are 4 unknown values a. Each known point (x, y) gives an equation in terms of these 4 unknowns. For example: Test import numpy as np. x = np.array([1.0, 2.0, 3.0, 4.0]) -0.5000 y = x ** 3 0.0000 0.0000 0.5000 a polyfit_coeffs (x, y) print (f"{len(a.shape):d}") print (f"{len(a):d}") print (f" (a[0]:.4f}") print (f" (abs (a[1]):.4f}") print (f" (abs (a [2]):.4f}") print (f" {a [3]:.4f}") Result 34567 1 4 Answer: (penalty regime: 10, 20, 30, 40, 50, 60 %) Reset answer 1 import numpy as np 2 3 def polyfit_coeffs(x, y): Returns the coefficients a_i.. # Add code here.