Consider the following problem Bipartite-Perfect-Matching: Input: Undirected bipartite graph G = (V,E) with bipartition V = L R where |L| = |R| = n. Output: A perfect matching if one exists, and NO if none exist in G. A perfect matching is a subset S of edges where every vertex v V is incident exactly one edge in S. Here is an example of a bipartite graph with a perfect matching in dashed edges:

Explain how to reduce the Bipartite-Perfect-Matching problem to the max-flow problem. In other words, explain how to solve the bipartite perfect matching problem using the algorithm for solving max-flow as a black-box.

Part (a): Given an input G = (V,E) to the Bipartite-Perfect-Matching problem, explain how you create the input to the max-flow problem (specify the graph G' and the edge capacities in this new graph). Do not do it for the above example, do it in general.

Part (b): Given a max-flow f* for the flow network that you defined in part (a), explain how you use f* to determine if G has a perfect matching.

Part (c): What is the running time of your algorithm in terms of the original graph G where n = |V | and m = |E|. State whether you are using the FordFulkerson or Edmonds-Karp algorithm (only consider these two which we saw in class); faster is better.

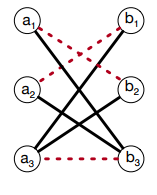
Part (d): A 2-perfect subgraph is a subset S of edges where every vertex has degree exactly 2 in S. So a perfect matching corresponds to a 1-perfect subgraph. Below is an example graph with a 2-perfect subgraph marked by red/dashed lines. Explain what needs to change in part (a) to check if a bipartite graph G has a 2-perfect subgraph.