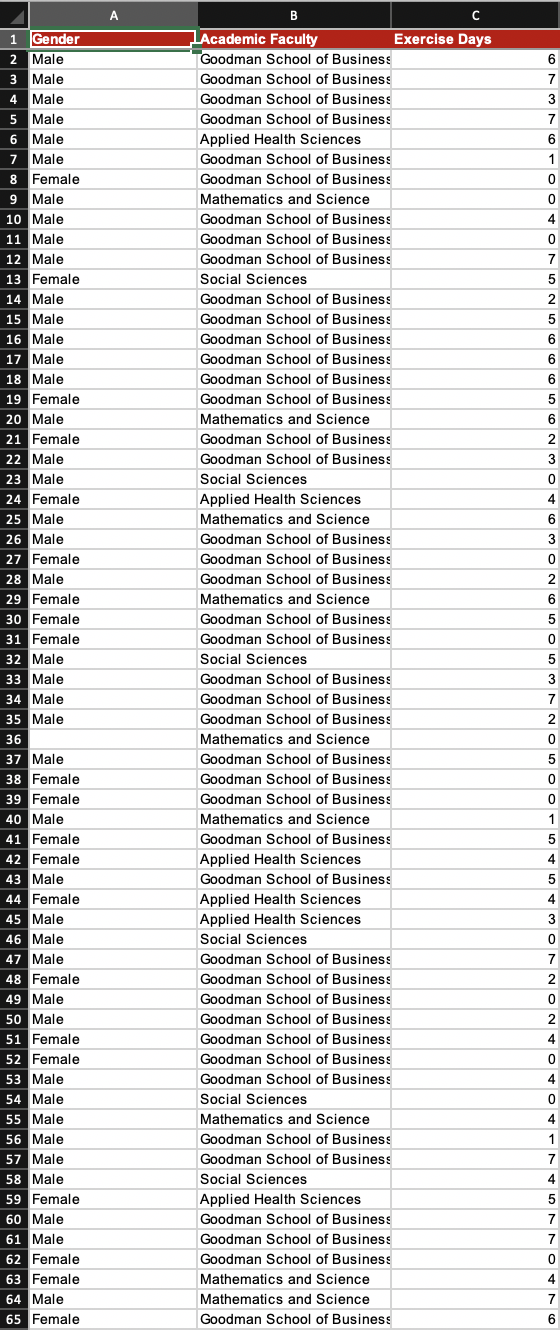
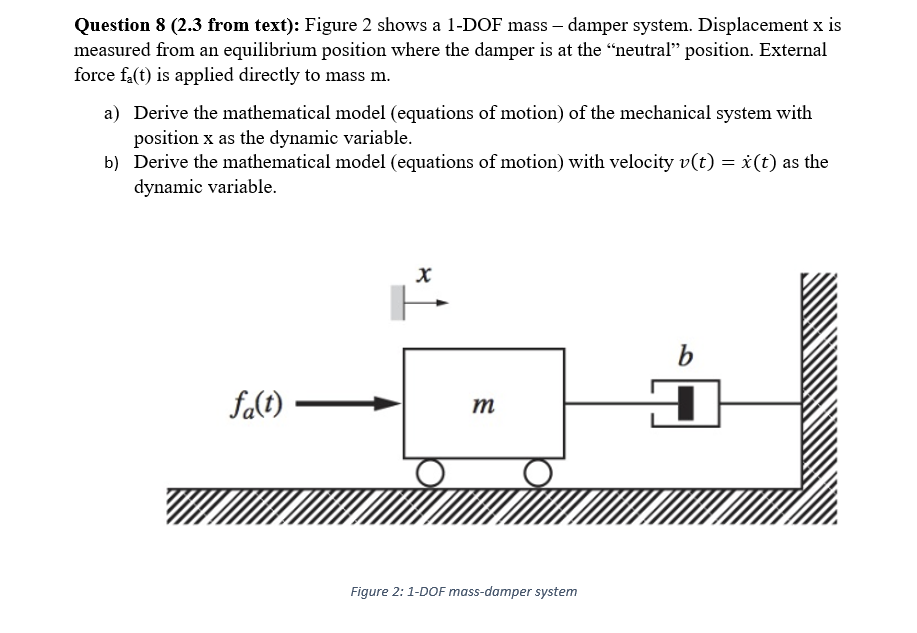
Consider the following questions
1. On Inverses using cofactor method (a) Compute the determinant, the cofactors matrix and the inverse (when exists), of the matrix A = 3.4. APPLICATIONS OF DETERMINANT 31 (b) Compute the determinant, the cofactors matrix and the inverse (when exists), of the matrix A = ( 12 ) (c) Compute the determinant, the cofactors matrix and the inverse (when exists), of the matrix A = ( a atl (d) Compute the determinant, the cofactors matrix and the inverse (when exists), of the matrix A = (2 2) (e) Compute the determinant, the cofactors matrix and the inverse (when exists), of the matrix A= 1 12. Write a program that uses parallel arrays to keep track of 5 courses. Each course will have a discipline code (like MTH or CS), a course number (use only integers), and a course title (like "Computer Science I"). There should be 5 functions: 1. intro ( ) - instructions about what is coming up 2. void fillCourses( ..... with parameters for the 3 arrays .... ) 3. int courseSearch( .... with parameter for the titles array and for a course title .... ) - the function returns -1 if the course title is not found; otherwise, it returns the element number of the array where the course title was found (There should be a prompt and input in the main() function, where the user enters a course title.) 4. void showCourses( .... with parameters for the 3 arrays ... ) 5. void showOneCourse( ... with parameters for the 3 arrays and for the element number of where the course searched for is found) - displays the discipline and course number of the course searched for. I SAMPLE RUNS:B C 1 Gender Academic Faculty Exercise Days Male Goodman School of Business Male Goodman School of Business Male Goodman School of Business 5 Male Goodman School of Business O - O V W V O 6 Male Applied Health Sciences Male Goodman School of Business 8 Female Goodman School of Business 9 Male Mathematics and Science 10 Male Goodman School of Business 11 Male Goodman School of Business 12 Male Goodman School of Business 13 Female Social Sciences 14 Male Goodman School of Business 15 Male Goodman School of Business 16 Male Goodman School of Business 17 Male Goodman School of Business 18 Male Goodman School of Business 19 Female Goodman School of Business 20 Male Mathematics and Science 21 Female Goodman School of Business 22 Male Goodman School of Business 23 Male Social Sciences 24 Female Applied Health Sciences 25 Male Mathematics and Science 26 Male Goodman School of Business 27 Female Goodman School of Business 28 Male Goodman School of Business 29 Female Mathematics and Science 30 Female Goodman School of Business Female A O A N O N N O W A U A U - O O U O N V W U O UT O N O W O A O W N O U O O ) U N O V O AO 31 Goodman School of Business 32 Male Social Sciences 33 Male Goodman School of Business 34 Male Goodman School of Business 35 Male Goodman School of Business 36 Mathematics and Science 37 Male Goodman School of Business 38 Female Goodman School of Business 39 Female Goodman School of Business 40 Male Mathematics and Science 41 Female Goodman School of Business 42 Female Applied Health Sciences 43 Male Goodman School of Business 44 Female Applied Health Sciences 45 Male Applied Health Sciences 46 Male Social Sciences 47 Male Goodman School of Business 48 Female Goodman School of Business 49 Male Goodman School of Business 50 Male Goodman School of Business 51 Female Goodman School of Business 52 Female Goodman School of Business 53 Male Goodman School of Business 54 Male Social Sciences o 55 Male Mathematics and Science 56 Male Goodman School of Business 57 Male Goodman School of Business Social Sciences VVU A V - A 58 Male 59 Female Applied Health Sciences 60 Male Goodman School of Business 61 Male Goodman School of Business 62 Female Goodman School of Business lo 63 Female Mathematics and Science OVA 64 Male Mathematics and Science 65 Female Goodman School of BusinessQuestion 8 (2.3 from text): Figure 2 shows a l-DOF mass damper system. Displacement x is measured 'om an equilibrium position where the damper is at the \"neutral\" position. External force fa(t) is applied directly to mass m. a) Derive the mathematical model (equations of motion) of the mechanical system with position X as the dynamic variable. b] Derive the mathematical model (equations of motion) with velocity v(t) : bit) as the dynamic variable. I '_. b ~ - 0-. Figure 2: lDOF massdamper system