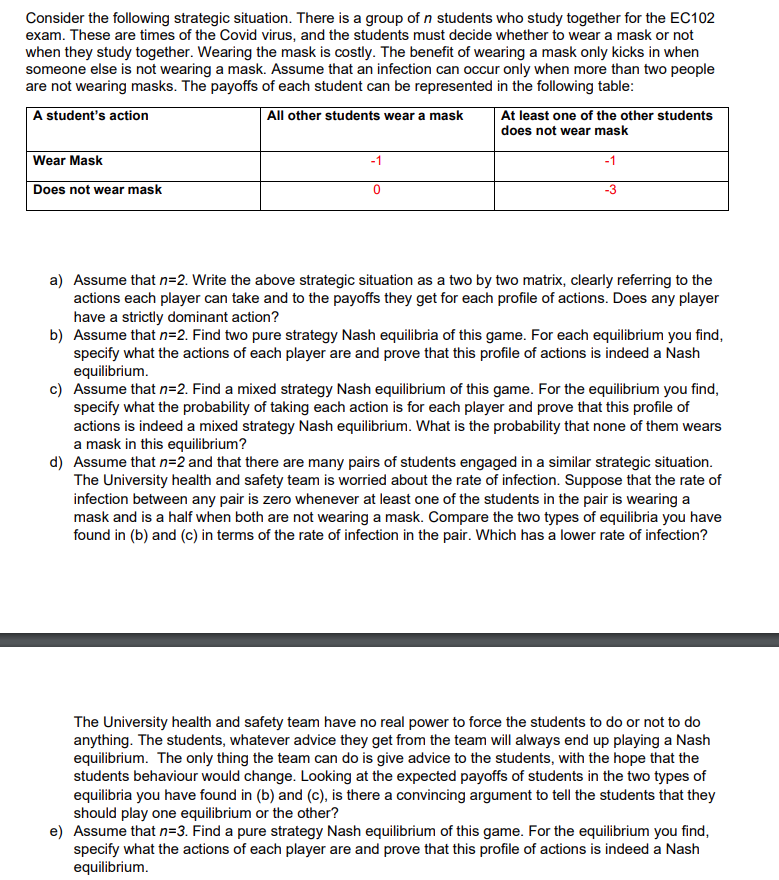
Consider the following strategic situation. There is a group of n students who study together for the EC1D2 exam. These are times of the lCovid virus1 and the students must decide whether to wear a mask or not when they study together. Wearing the mask is costly. The benefit of wearing a mask only kicks in when someone else is not wearing a mask. Assume that an infection can occur only when more than two people are not wearing masks. The payoffs of each student can be represented in the following table: A student's action All other students wear a mask At least one of the other students does not wear mask a] Assume that n=2. Write the above strategic situation as a two by two matrix1 clearly referring to the actions each player can take and to the payoffs they get for each prole of actions. Does any player have a strictly dominant action? b] Assume that n=2. Find two pure strategy Nash equilibria of this game. For each equilibrium you nd, specify what the actions of each player are and prove that this prole of actions is indeed a Nash equiliblium. c} Assume that n=2. Find a mixed strategy Nash equilibrium of this game. For the equilibrium you nd, specify what the probability of taking each action is for each player and prove that this prole of actions is indeed a mixed strategy Nash equilibrium. What is the probability that none of them wears a mask in this equilibrium? d] Assume that n=2 and that there are many pairs of students engaged in a similar strategic situation. The University health and safety team is worried about the rate of infection. Suppose that the rate of infection between any pair is zero whenever at least one of the students in the pair is wearing a mask and is a half when both are not wearing a mask. Compare the two types of equilibria you have found in {b} and {c} in terms of the rate of infection in the pair. Which has a lower rate of infection? The University health and safety team have no real power to force the students to do or not to do anything. The students, whatever advice they get from the team will always end up playing a Nash equiliblium. The only thing the team can do is give advice to the students. with the hope that the students behaviour would change. Looking at the expected payoffs of students in the two types of equiliblia you have found in (b) and {c}, is there a convincing argument to tell the students that they should play one equilibrium or the other? e] Assume that n=3. Find a pure strategy Nash equilibrium ofthis game. For the equilibrium you nd1 specify what the actions of each player are and prove that this prole of actions is indeed a Nash equiliblium