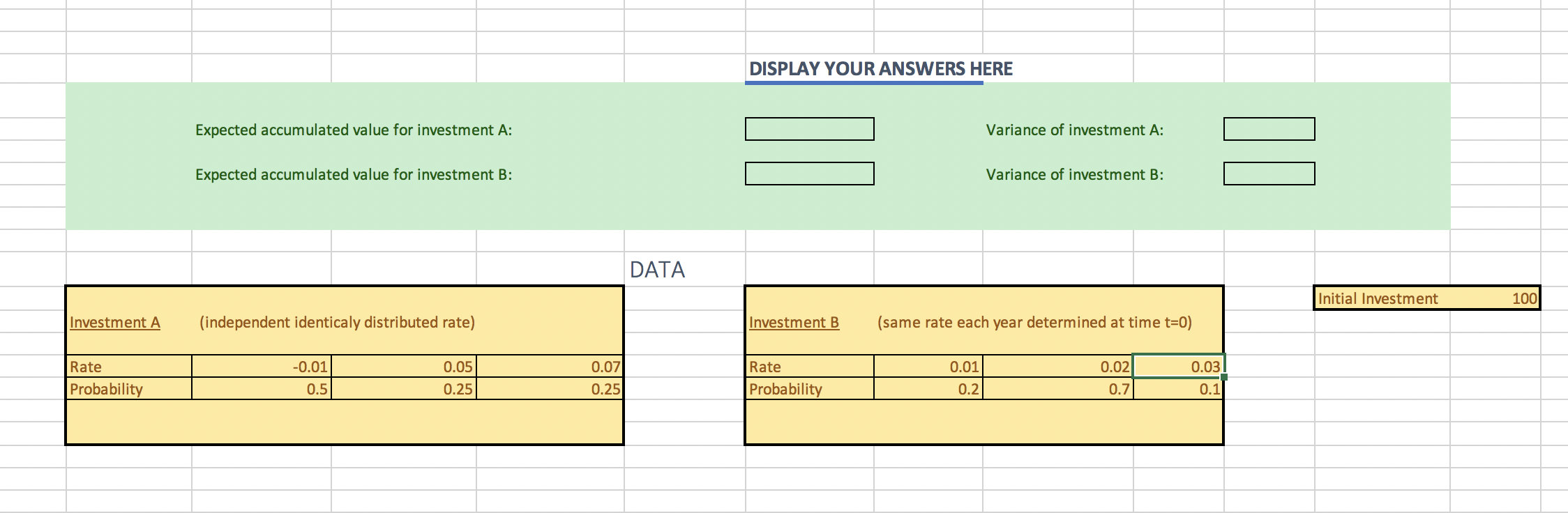
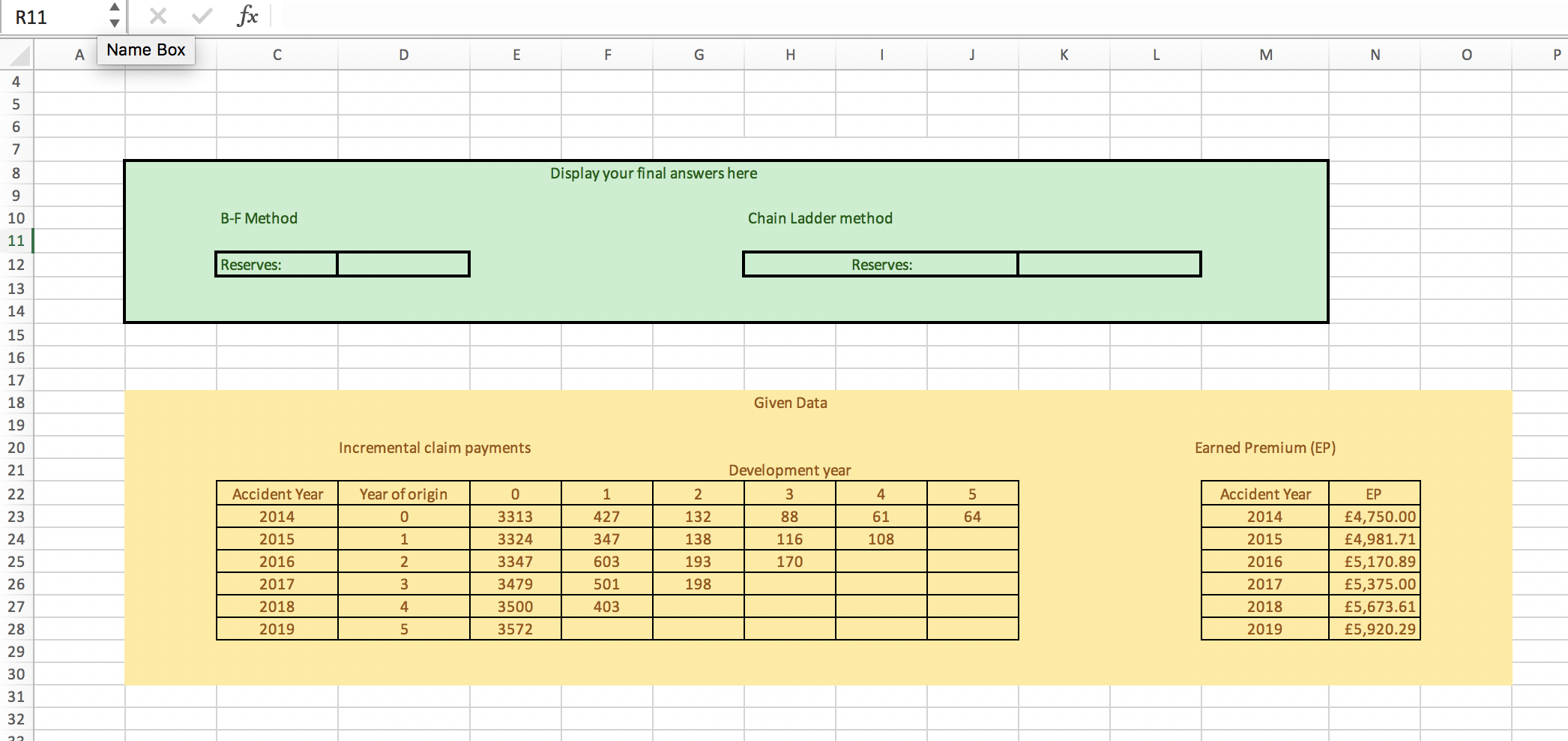
Consider the following two 4-year investments, with same initial investment given in the spread- sheet: Investment A: In each year, the annual effective rate of return (or rate, for short) is a discrete random variable. The rates in each year are independent and identically distributed, and their probability distribution given in the spreadsheet. Investment B: In year 1, the annual effective rate of return (or rate, for short) is a discrete random variable. The probability distribution of the rate is given in the spreadsheet. Once the rate is chosen for the first year, it stays fixed for the next years. Calculate the expected accumulated value and variance after 4 years under each investment. In your report you should include the following: State the expected accumulated value and variance for each investment. Discuss which investment is safer and which one riskier, and why. DISPLAY YOUR ANSWERS HERE Expected accumulated value for investment A: Variance of investment A: Expected accumulated value for investment B: Variance of investment B: DATA Initial Investment 100 Investment A (independent identicaly distributed rate) Investment B (same rate each year determined at time t=0) 0.07 Rate Probability -0.01 0.5 0.05 0.25 Rate Probability 0.01 0.2 0.02 0.7 0.03 0.1 0.25 R11 x fx A Name Box D E F G H j L M N o P 4 5 6 7 8 Display your final answers here B-F Method Chain Ladder method 9 10 11 12 Reserves: Reserves: 13 14 15 16 17 18 Given Data 19 20 21 Incremental claim payments Earned Premium (EP) Development year 3 22 0 1 2 4 5 Year of origin 0 Accident Year 2014 23 88 61 64 3313 3324 132 138 24 1 116 108 2015 Accident Year 2014 2015 2016 2017 2018 2019 427 347 603 501 2 170 25 26 2016 193 198 EP 4,750.00 4,981.71 5,170.89 5,375.00 5,673.61 5,920.29 3 3347 3479 3500 3572 2017 27 4 403 2018 28 5 2019 29 30 31 32 Consider the Bornhuetter-Ferguson method and the chain ladder method in the context of de- velopment claims in insurance'. Apply the two methods to the dataset given on the spreadsheet in order to find the reserve required in 2019. Note that figures are incremental claims in the past 5 years, and you should assume that 2014 claims have completely run off in 2019. In your report you should state the reserve required for both methods. Consider the following two 4-year investments, with same initial investment given in the spread- sheet: Investment A: In each year, the annual effective rate of return (or rate, for short) is a discrete random variable. The rates in each year are independent and identically distributed, and their probability distribution given in the spreadsheet. Investment B: In year 1, the annual effective rate of return (or rate, for short) is a discrete random variable. The probability distribution of the rate is given in the spreadsheet. Once the rate is chosen for the first year, it stays fixed for the next years. Calculate the expected accumulated value and variance after 4 years under each investment. In your report you should include the following: State the expected accumulated value and variance for each investment. Discuss which investment is safer and which one riskier, and why. DISPLAY YOUR ANSWERS HERE Expected accumulated value for investment A: Variance of investment A: Expected accumulated value for investment B: Variance of investment B: DATA Initial Investment 100 Investment A (independent identicaly distributed rate) Investment B (same rate each year determined at time t=0) 0.07 Rate Probability -0.01 0.5 0.05 0.25 Rate Probability 0.01 0.2 0.02 0.7 0.03 0.1 0.25 R11 x fx A Name Box D E F G H j L M N o P 4 5 6 7 8 Display your final answers here B-F Method Chain Ladder method 9 10 11 12 Reserves: Reserves: 13 14 15 16 17 18 Given Data 19 20 21 Incremental claim payments Earned Premium (EP) Development year 3 22 0 1 2 4 5 Year of origin 0 Accident Year 2014 23 88 61 64 3313 3324 132 138 24 1 116 108 2015 Accident Year 2014 2015 2016 2017 2018 2019 427 347 603 501 2 170 25 26 2016 193 198 EP 4,750.00 4,981.71 5,170.89 5,375.00 5,673.61 5,920.29 3 3347 3479 3500 3572 2017 27 4 403 2018 28 5 2019 29 30 31 32 Consider the Bornhuetter-Ferguson method and the chain ladder method in the context of de- velopment claims in insurance'. Apply the two methods to the dataset given on the spreadsheet in order to find the reserve required in 2019. Note that figures are incremental claims in the past 5 years, and you should assume that 2014 claims have completely run off in 2019. In your report you should state the reserve required for both methods