Question: Consider the integral '3 [1 In(x) dx dy. (a) If we want to evaluate this integral, why do we need to change the order

Consider the integral '3 [1 In(x) dx dy. (a) If we want

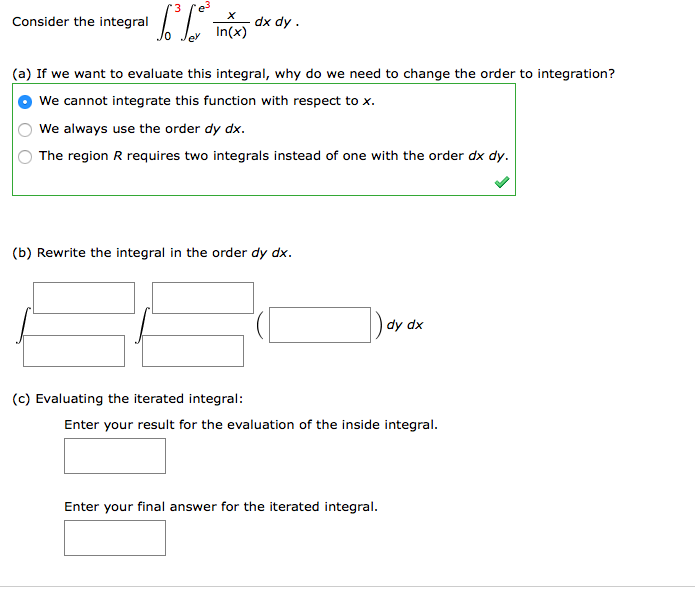
Consider the integral '3 [1 In(x) dx dy. (a) If we want to evaluate this integral, why do we need to change the order to integration? We cannot integrate this function with respect to x. We always use the order dy dx. The region R requires two integrals instead of one with the order dx dy. (b) Rewrite the integral in the order dy dx. (c) Evaluating the iterated integral: dy dx Enter your result for the evaluation of the inside integral. Enter your final answer for the iterated integral.

Step by Step Solution

★★★★★

3.28 Rating (145 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

If we want to maximize profit, why do we use unit contribution margin s in our analysis instead of unit gross margins?

If we want to determine whether the proportions of customers who favor each of four different designer handbags are all the same, we could conduct a experiment Multiple choice question multinomial...

If we want to evaluate the integral x+40 I = dx, + 64 we use the trigonometric substitution x = 2 tan(0) and dx = de and therefore the integral becomes, in terms of 0, I = de The antiderivative in...

Math 1172 Project #1 Applications of Integration Due: Tuesday, September 12 Name(s): - - - - - - - - - - - - - - - - - - - - Description - - - - - - - - - - - - - - - - - - - The definite integral is...

Section 8.3 Reading Assignment: Trigonometric Integrals Answer Only Exercise 1, 2, and 3 by using a screenshot provided Calculus Pearson textbook. Make sure you read these three questions very...

Question 1: Summarize the Riemann sum argument that gives the formula of area as a double integral. When computing these, you might have memories of Calculus I and finding the area of regions. This...

Question 2: Explain geometrically how the formula for a single A is obtained. Explain why this area depends on r and not just r. Note that this is about just a single "polar rectangle" and not the...

Feedback: #1: This is not the argument in this reading passage. (0/4). Question 1: Summarize the Riemann sum argument that gives the formula of area as a double integral. Hint 1: Read the subsection...

You have recently been appointed as the Store Manager of the Australian Hardware Newcastle store. You and the COO (Chief Operating Officer) have discussed opportunities for you to make an impact and...

1. If a firm has an after-tax profit margin of 6%, an asset turnover of 3.0 times and no debt, what will be its return on return on equity? 2. Your cousin will sell you his coffee shop for $30,000,...

A business that is procedurally complex and involves managing a wide variety of details may be appropriate for individuals who are Blank _ _ _ _ _ _ . Multiple choice question. detail oriented...

Industrial Construction Co. wanted to raise money to construct a canning factory in Wisconsin. Various persons promised to subscribe the needed amount, which they agreed to pay when the construction...

Zoya operated a store in premises rented from Peerless. The lease required Zoya to maintain liability insurance to protect Zoya and Peerless. Caswell entered the store, fell through a trap door, and...

Martin made an oral contract with Cresheim Garage to work as its manager for two years. Cresheim wrote Martin a letter stating that the oral contract had been made and setting forth all of its terms....

The file accounting partners contains the number of partners in a cohort of rising accounting firms that have a tagged as firms to watch The firms have the following numbers of partners: a. Compute...

Revenue and expense data for the current calendar year for Garrity Electronics Company and for the electronics industry are as follows. The Garrity Electronics Company data are expressed in dollars....

what is the answer to this? .. W2.5 - Quiz X Question 3 - W2.5 - Quiz - Cc x * Chat Thread X 1+ C 2% ezto.mheducation.com/ext/map/index.html?_con=con external_browser=0 launchUrl=https To exit full...

Use a graphing device as in Example 4 (or Newtons method or solve numerically using a calculator or computer) to find the critical points of f correct to three decimal places. Then classify the...

Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. For any vectors u and v in V 3 , u v = v u.

Determine whether each integral is convergent or divergent. Evaluate those that are convergent.

Bond C and Bond D both have a face value of $1000, and each carries a 4.2% coupon. Bond C matures in 3 years and Bond B matures in 23 years. If the prevailing required rate of return in the bond...

Refer to the Why Divide by n - 1 applet. The first applet on the page randomly selects sample of n = 3 from a population in which the standard deviation is = 29.2. a. A sample consisting of n = 3...

Use the second Building a Box Plot applet to construct a box plot for the data in Example 2.13. a. How would you describe the shape of the data distribution? b. Use the box plot to approximate the...