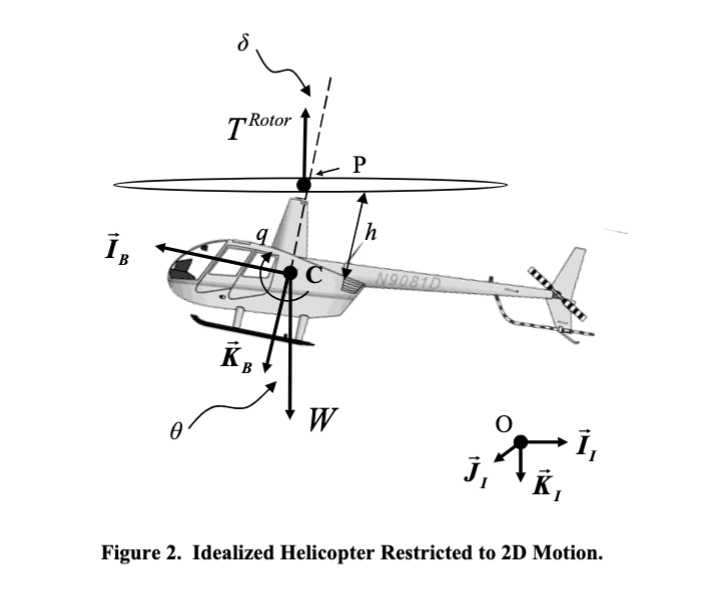
Consider the pitching motion in a 2D plane of an idealized helicopter, shown in Figure 2. Only two external forces act on the helicopter. The first force is the thrust of the rotor which has magnitude Rotor, and acts at a point P which is h above the center of mass C. The thrust force is tilted forward with respect to the body KB axis as shown in the figure by an angle d. The second external force is gravity which has magnitude W and acts at the center of mass. The velocity of point C is vc/ = u + v] + w, and the velocity of point P is VP/I = UpB + VP]B + WpKg. The mass of the helicopter is m, and it is symmetric about the IB - KB plane. The pitch moment of inertia about C in the body frame is Iyy. For this analysis, the machine is restricted to move in a plane, so = y=p=r=v=vp = 0 (helicopter can change pitch attitude, move fore/aft, and up/down, but no other motion is allowed). The body has three degrees of freedom - two translational degrees of freedom and one rotational. Derive the two translational dynamic equations (equations for u and w) and the rotational dynamic equation (equation for ) as a function of the given parameters and force magnitudes Rotor and W. (13 points) TRotor P A h 1x KB W N9081D J Figure 2. Idealized Helicopter Restricted to 2D Motion.