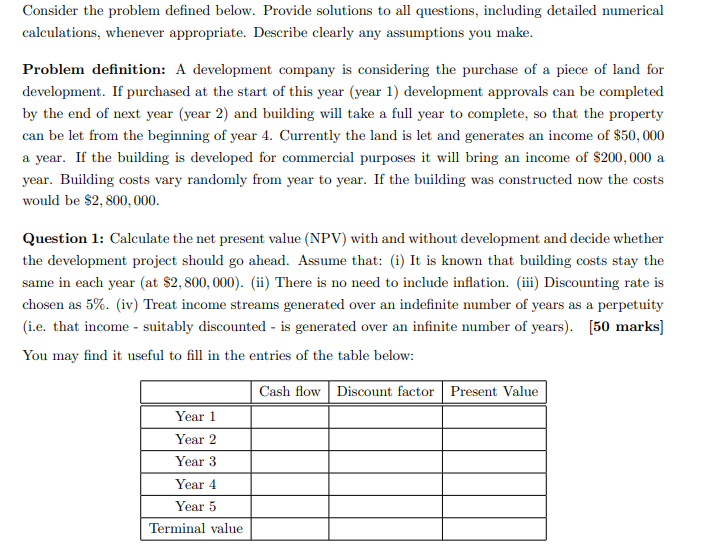

Consider the problem defined below. Provide solutions to all questions, including detailed numerical calculations, whenever appropriate. Describe clearly any assumptions you make. Problem definition: A development company is considering the purchase of a piece of land for development. If purchased at the start of this year (year 1) development approvals can be completed by the end of next year (year 2) and building will take a full year to complete, so that the property can be let from the beginning of year 4. Currently the land is let and generates an income of $50,000 a year. If the building is developed for commercial purposes it will bring an income of $200,000 a year. Building costs vary randomly from year to year. If the building was constructed now the costs would be $2,800,000. Question 1: Calculate the net present value (NPV) with and without development and decide whether the development project should go ahead. Assume that: (i) It is known that building costs stay the same in each year (at $2,800,000). (ii) There is no need to include inflation. (iii) Discounting rate is chosen as 5%. (iv) Treat income streams generated over an indefinite number of years as a perpetuity (i.e. that income - suitably discounted - is generated over an infinite number of years). [50 marks) You may find it useful to fill in the entries of the table below: Cash flow Discount factor Present Value Year 1 Year 2 Year 3 Year 4 Year 5 Terminal value Question 2: Suppose that the decision on whether or not to build is made at the beginning of Year 3 depending on a bid of the total building costs) made by a building company. Determine the maximum bid value for which it is worth going ahead with the development. [20 marks) Question 3: Suppose that random variable X is normally distributed, i.e. X~40). Show that: E(max(a x,0)) = ado(a) - Puso (2)da - where Powe(a) = vztof exp (6) V22 and mola) = $mw (a )des P Hence show that: E(max(a X,0)) = (a -... (a) +0,(a) [10 marks) 1 Question 4: Assume that the building costs are normally distributed with mean y = 2,800K and standard deviation o = 200K. and that this is known from the beginning of Year 1. Determine the expected value of the investment and decide whether the project is worth going ahead. Investigate if the decision is still valid if x = 2,800K but o varies by +10% from its stated value. (Hint: Use the result stated in Question 3 above], [20 marks] Table of Normal Distribution cdf (2) (2) letra /2 Consider the problem defined below. Provide solutions to all questions, including detailed numerical calculations, whenever appropriate. Describe clearly any assumptions you make. Problem definition: A development company is considering the purchase of a piece of land for development. If purchased at the start of this year (year 1) development approvals can be completed by the end of next year (year 2) and building will take a full year to complete, so that the property can be let from the beginning of year 4. Currently the land is let and generates an income of $50,000 a year. If the building is developed for commercial purposes it will bring an income of $200,000 a year. Building costs vary randomly from year to year. If the building was constructed now the costs would be $2,800,000. Question 1: Calculate the net present value (NPV) with and without development and decide whether the development project should go ahead. Assume that: (i) It is known that building costs stay the same in each year (at $2,800,000). (ii) There is no need to include inflation. (iii) Discounting rate is chosen as 5%. (iv) Treat income streams generated over an indefinite number of years as a perpetuity (i.e. that income - suitably discounted - is generated over an infinite number of years). [50 marks) You may find it useful to fill in the entries of the table below: Cash flow Discount factor Present Value Year 1 Year 2 Year 3 Year 4 Year 5 Terminal value Question 2: Suppose that the decision on whether or not to build is made at the beginning of Year 3 depending on a bid of the total building costs) made by a building company. Determine the maximum bid value for which it is worth going ahead with the development. [20 marks) Question 3: Suppose that random variable X is normally distributed, i.e. X~40). Show that: E(max(a x,0)) = ado(a) - Puso (2)da - where Powe(a) = vztof exp (6) V22 and mola) = $mw (a )des P Hence show that: E(max(a X,0)) = (a -... (a) +0,(a) [10 marks) 1 Question 4: Assume that the building costs are normally distributed with mean y = 2,800K and standard deviation o = 200K. and that this is known from the beginning of Year 1. Determine the expected value of the investment and decide whether the project is worth going ahead. Investigate if the decision is still valid if x = 2,800K but o varies by +10% from its stated value. (Hint: Use the result stated in Question 3 above], [20 marks] Table of Normal Distribution cdf (2) (2) letra /2








