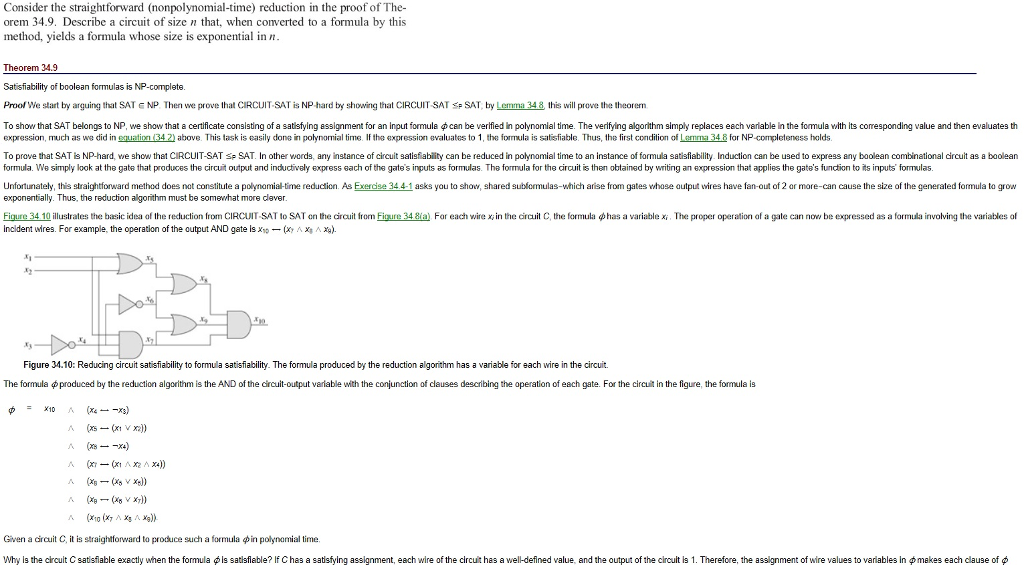
Consider the straightforward (nonpolynomial-time) reduction in the proof of Theorem 34.9. Describe a circuit of size n that, when converted to a formula by this method, yields a formula whose size is exponential in n. Theorem 34.9 Satisfiability of boolean formulas is NP-complete. Proof We start by arguing that SAT elementof NP. Then we prove that CIRCUIT SAT is NP hard by showing that CIRCUIT SAT SAT, by Lemma 34.8 this will prove the theorem. To show that SAT belongs to NP, we show that a certificate consisting of a satisfying assignment for an input formula can be verified in polynomial time. The verifying algorithm simply replaces each variable in the formula with its corresponding value and then evaluates expression, much as we did in equation (34 2) above. This task is easily done in polynomial time. If the expression evaluates to 1, the formula is satisfiable. Thus, the first condition of Lemma 34.8 for NP completeness holds. To prove that SAT is NP-hard, we show that CIRCUIT-SAT SAT. In other words, any instance of circuit satisfiability can be reduced in polynomial time to an instance of formula satisfiability. Induction can be used to express any boolean combinational circuit as a boolean formula. We simply look at the gate that produces the circuit output and inductively express each of the gate's inputs as formulas. The formula for the circuit is then obtained by writing an expression that applies the gate's function to its inputs' formulas. Unfortunately, this straightforward method does not constitute a polynomial-time reduction. As Exercise 34 4-1 asks you to show, shared subformulas-which arise from gates whose output wires have fan-out of 2 or more-can cause the size of the generated formula to grow exponentially. Thus, the reduction algorithm must be somewhat more clever. Figure 34 10 illustrates the basic idea of the reduction from CIRCUIT SAT to SAT on the circuit from Figure 348a) For each wire in the circuit C, the formula Phi has a variable x The proper operation of a gate can now be expressed as a formula involving the variables of incident wires. For example, the operation of the output AND gate is x_10 - (x ^x ^x). The formula Phi produced by the reduction algorithm is the AND of the circuit-output variable with the conjunction of clauses describing the operation of each gate. For the circuit in the figure the formula is Phi = x_10 Lambda (x_4 - not x_8) Lambda (x_5 - (x_1 x_2) Lambda (x_8 - not x_4) Lambda (x_7 - (x_1 6 x_2 Lambda x_4)) Lambda (x_6 - (x x)) Lambda (x_8 - (x_5 x_5)) (x_8 - (x_6 x_7)) Lambda (x_10 (x_7 Lambda x_8 Lambda x_9)). Given a circuit C, it is straightforward to produce such a formula Phi in polynomial time. Why is the circuit C satisfiable exactly when the formula Phi is satisfiable? If C has a satisfying assignment, each wire of the circuit has a well-defined value, and the output of the circuit is 1. Therefore, the assignment of wire values to variables in makes each clause of Phi Consider the straightforward (nonpolynomial-time) reduction in the proof of Theorem 34.9. Describe a circuit of size n that, when converted to a formula by this method, yields a formula whose size is exponential in n. Theorem 34.9 Satisfiability of boolean formulas is NP-complete. Proof We start by arguing that SAT elementof NP. Then we prove that CIRCUIT SAT is NP hard by showing that CIRCUIT SAT SAT, by Lemma 34.8 this will prove the theorem. To show that SAT belongs to NP, we show that a certificate consisting of a satisfying assignment for an input formula can be verified in polynomial time. The verifying algorithm simply replaces each variable in the formula with its corresponding value and then evaluates expression, much as we did in equation (34 2) above. This task is easily done in polynomial time. If the expression evaluates to 1, the formula is satisfiable. Thus, the first condition of Lemma 34.8 for NP completeness holds. To prove that SAT is NP-hard, we show that CIRCUIT-SAT SAT. In other words, any instance of circuit satisfiability can be reduced in polynomial time to an instance of formula satisfiability. Induction can be used to express any boolean combinational circuit as a boolean formula. We simply look at the gate that produces the circuit output and inductively express each of the gate's inputs as formulas. The formula for the circuit is then obtained by writing an expression that applies the gate's function to its inputs' formulas. Unfortunately, this straightforward method does not constitute a polynomial-time reduction. As Exercise 34 4-1 asks you to show, shared subformulas-which arise from gates whose output wires have fan-out of 2 or more-can cause the size of the generated formula to grow exponentially. Thus, the reduction algorithm must be somewhat more clever. Figure 34 10 illustrates the basic idea of the reduction from CIRCUIT SAT to SAT on the circuit from Figure 348a) For each wire in the circuit C, the formula Phi has a variable x The proper operation of a gate can now be expressed as a formula involving the variables of incident wires. For example, the operation of the output AND gate is x_10 - (x ^x ^x). The formula Phi produced by the reduction algorithm is the AND of the circuit-output variable with the conjunction of clauses describing the operation of each gate. For the circuit in the figure the formula is Phi = x_10 Lambda (x_4 - not x_8) Lambda (x_5 - (x_1 x_2) Lambda (x_8 - not x_4) Lambda (x_7 - (x_1 6 x_2 Lambda x_4)) Lambda (x_6 - (x x)) Lambda (x_8 - (x_5 x_5)) (x_8 - (x_6 x_7)) Lambda (x_10 (x_7 Lambda x_8 Lambda x_9)). Given a circuit C, it is straightforward to produce such a formula Phi in polynomial time. Why is the circuit C satisfiable exactly when the formula Phi is satisfiable? If C has a satisfying assignment, each wire of the circuit has a well-defined value, and the output of the circuit is 1. Therefore, the assignment of wire values to variables in makes each clause of Phi