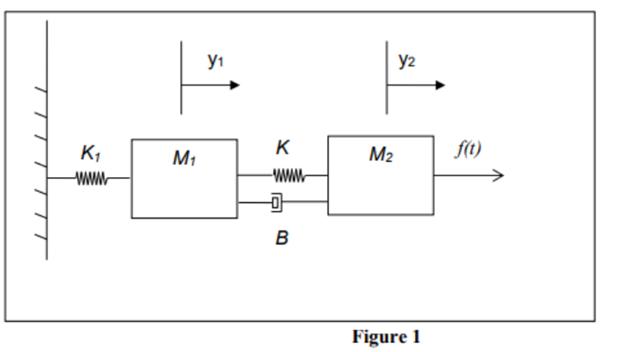
Consider the system in Figure 1. Mi and M2 are two masses. K and Ki are the spring constants and B is a damper. Simulate results for 50s. Determine the differential equations that govern the behaviour of the system in Figure 1. [10 marks] Determine a state-space representation for the system. Select the displacements, y and y2, and the velocities, v and v2, as the states. Select y, as the output. [20 marks] Form the transfer function for the system that relates the Laplace transform of y(t) to the Laplace transform of (). [20 marks] Form the transfer function for the system that relates the Laplace transform of y2(t) to the Laplace transform of ft). [10 marks] Simulate the system using the state-space representation. Set Mi=3, M2-6, K=2, Ki=5 and B-3. Determine the unit-impulse response for y(t) and y2(t). [10 marks] Simulate the same system using the Laplace transforms and confirm that the same results are obtained for the unit-impulse responses as are obtained using the state- space representation. [10 marks] Determine the poles of the system and comment on the stability of the system. [10 marks] y1 y2 K; M1 K M2 f(t) B Figure 1