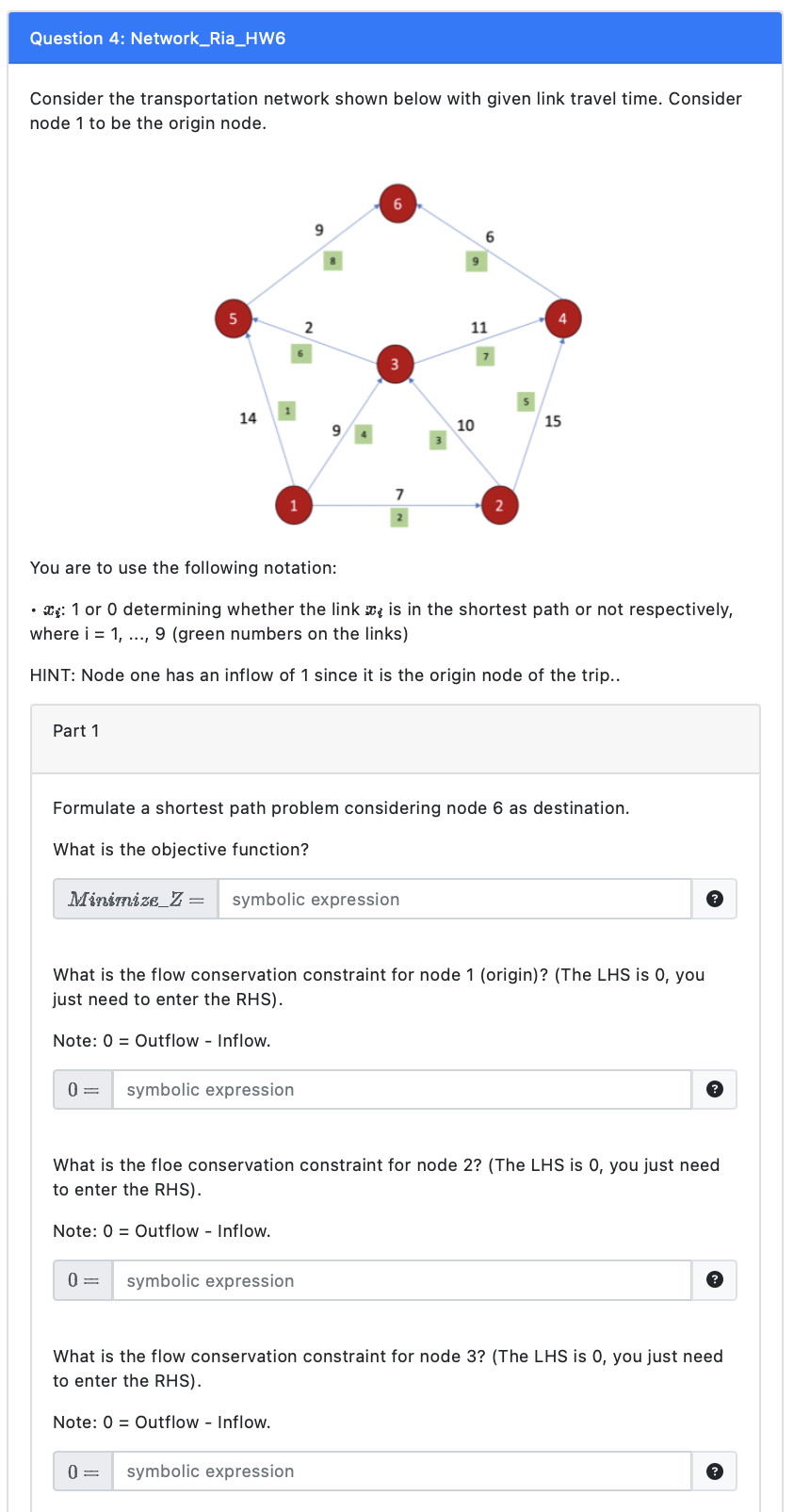
Consider the transportation network shown below with given link travel time. Consider node 1 to be the origin node. You are to use the following notation: - xi:1 or 0 determining whether the link xi is in the shortest path or not respectively, where i=1,,9 (green numbers on the links) HINT: Node one has an inflow of 1 since it is the origin node of the trip.. Part 1 Formulate a shortest path problem considering node 6 as destination. What is the objective function? Minsinize_Z = What is the flow conservation constraint for node 1 (origin)? (The LHS is 0 , you just need to enter the RHS). Note: 0 = Outflow - Inflow. What is the floe conservation constraint for node 2? (The LHS is 0 , you just need to enter the RHS). Note: 0 = Outflow - Inflow. 0 What is the flow conservation constraint for node 3 ? (The LHS is 0 , you just need to enter the RHS). Note: 0= Outflow - Inflow. What is the flow conservation constraint for node 4 ? (The LHS is 0 , you just need to enter the RHS). Note: 0= Outflow - Inflow. What is the flow conservation constraint for node 5 ? (The LHS is 0 , you just need to enter the RHS). Note: 0= Outflow - Inflow. What is the flow conservation constraint for node 6 (destination)? (The LHS is 0 , you just need to enter the RHS). Note: 0 = Outflow - Inflow. Node 6 has an outflow of 1 since it is the destination node of this trip. Part 2 Now, solve the shortest path problem from node 1 to all nodes (different nodes as destinations) and specify the respective total travel time. Node 1 to Node 2 Node 1 to Node 3 Node 1 to Node 4 Node 1 to Node 5 Node 1 to Node 6 Consider the transportation network shown below with given link travel time. Consider node 1 to be the origin node. You are to use the following notation: - xi:1 or 0 determining whether the link xi is in the shortest path or not respectively, where i=1,,9 (green numbers on the links) HINT: Node one has an inflow of 1 since it is the origin node of the trip.. Part 1 Formulate a shortest path problem considering node 6 as destination. What is the objective function? Minsinize_Z = What is the flow conservation constraint for node 1 (origin)? (The LHS is 0 , you just need to enter the RHS). Note: 0 = Outflow - Inflow. What is the floe conservation constraint for node 2? (The LHS is 0 , you just need to enter the RHS). Note: 0 = Outflow - Inflow. 0 What is the flow conservation constraint for node 3 ? (The LHS is 0 , you just need to enter the RHS). Note: 0= Outflow - Inflow. What is the flow conservation constraint for node 4 ? (The LHS is 0 , you just need to enter the RHS). Note: 0= Outflow - Inflow. What is the flow conservation constraint for node 5 ? (The LHS is 0 , you just need to enter the RHS). Note: 0= Outflow - Inflow. What is the flow conservation constraint for node 6 (destination)? (The LHS is 0 , you just need to enter the RHS). Note: 0 = Outflow - Inflow. Node 6 has an outflow of 1 since it is the destination node of this trip. Part 2 Now, solve the shortest path problem from node 1 to all nodes (different nodes as destinations) and specify the respective total travel time. Node 1 to Node 2 Node 1 to Node 3 Node 1 to Node 4 Node 1 to Node 5 Node 1 to Node 6