Answered step by step
Verified Expert Solution
Question
1 Approved Answer
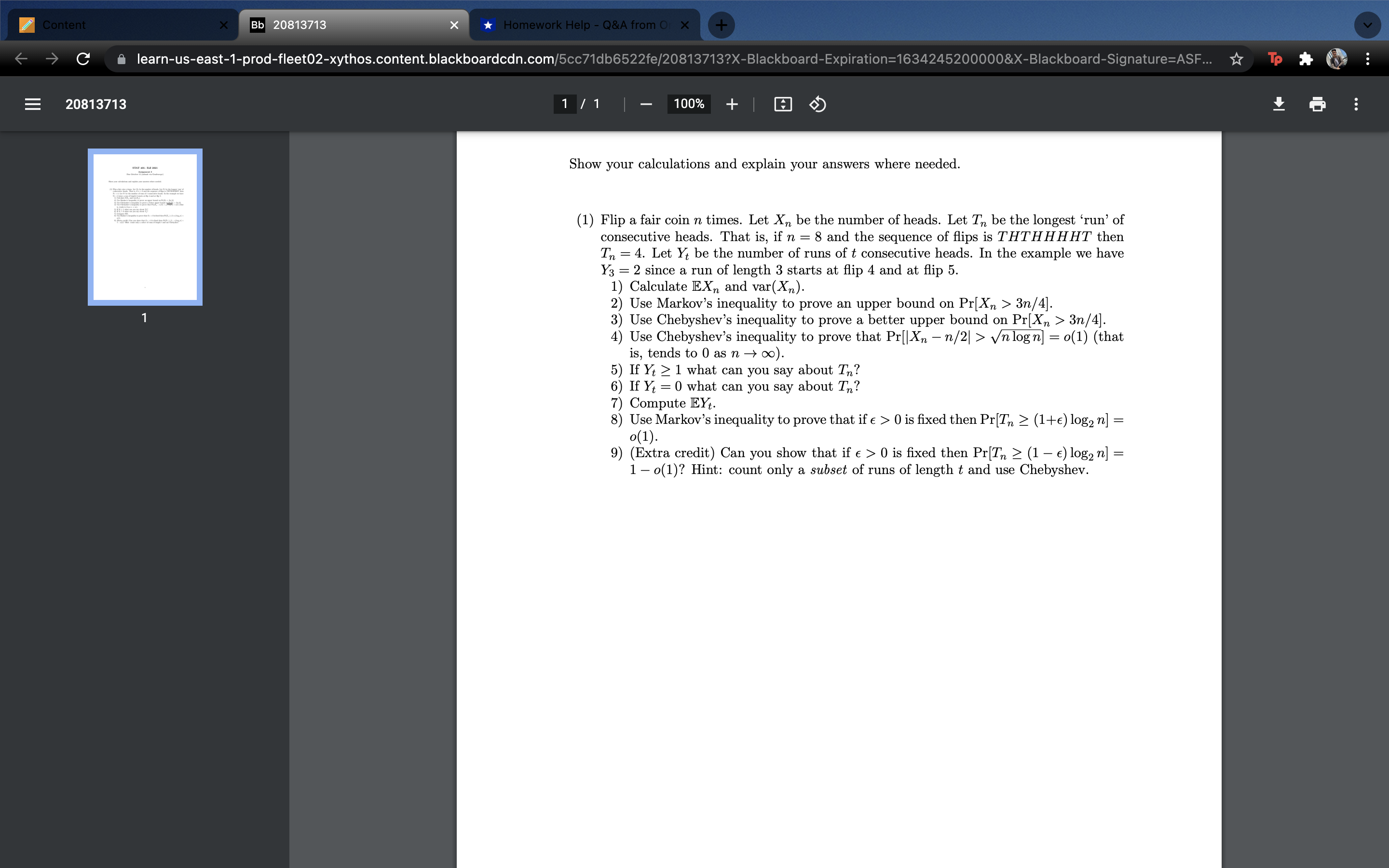
Content Bb 20813713 Homework Help - Q&A from Or X C learn-us-east-1-prod-fleet02-xythos.content.blackboardcdn.com/5cc71db6522fe/20813713?X-Blackboard-Expiration=1634245200000&X-Blackboard-Signature=ASF... To E 20813713 1 / 1 | - 100% + Show your calculations
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


