Convolution layers in most CNNs consist of multiple input and output feature maps. The collection of kernels form a 4D tensor (output channels o, input channels i, filter rows k, filter columns k), represented in short as (o, i, k, k). For each output channel, each input channel is convolved with a distinct 2D slice of the 4D kernel and the resulting set of feature maps is summed element-wise to produce the corresponding output feature map.

There is an interesting property that a convolutional layer with kernel size (o r², i, k, k) is identical to a transposed convolution layer with kernel size (o, i, k r, k r). Here the word 'identical' means with the same input feature X, both operations will give the same output Y with only a difference in the ordering of flattened elements of Y .

Now let us prove the property in a restricted setting. Consider o = 1, r = 2, i = 1, k = 1. Given input feature X as

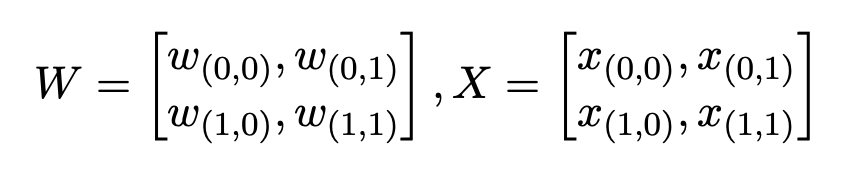
\f