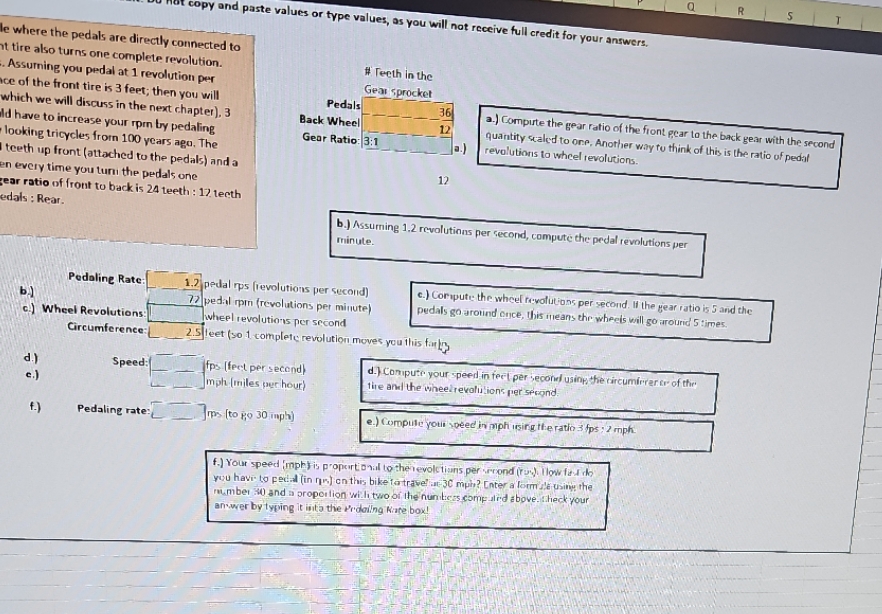
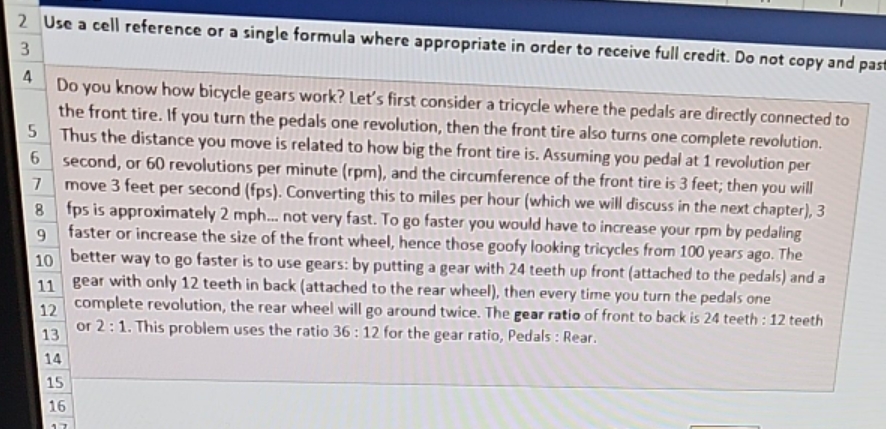
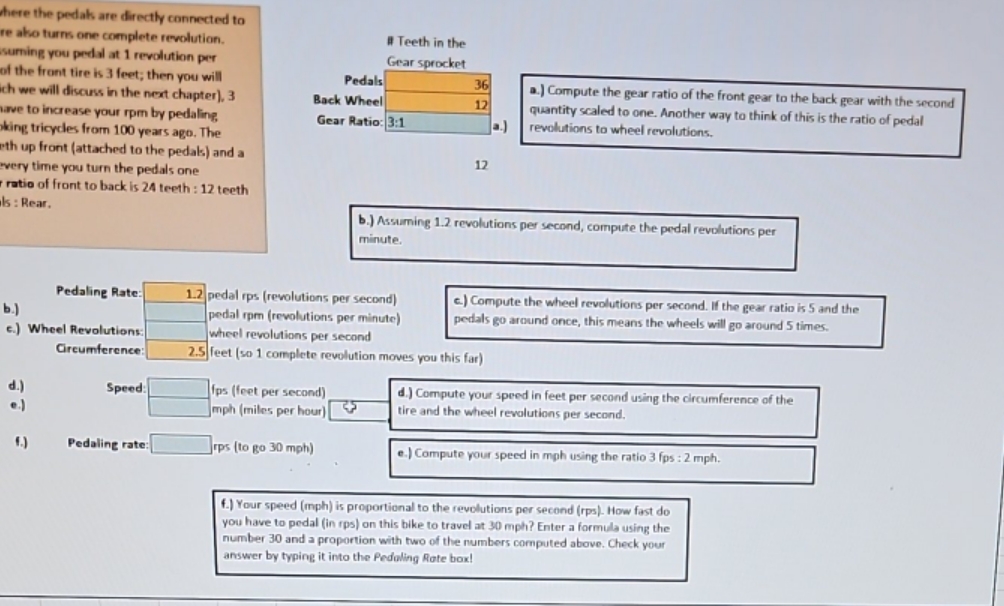
copy and paste values or type values, as you will not receive full credit for your answers. R S T le where the pedals are directly connected to t tire also turns one complete revolution. Assuming you pedal at 1 revolution per nce of the front tire is 3 feet; then you will which we will discuss in the next chapter), 3 ld have to increase your rpm by pedaling looking tricycles from 100 years ago. The teeth up front (attached to the pedals) and a en every time you turn the pedals one gear ratio of front to back is 24 teeth : 12 teeth edals: Rear. #Teeth in the Gear Sprocket Pedals 36 12 Gear Ratio: 3:1 Back Wheel 12 a) Compute the gear ratio of the front gear to the back gear with the second quantity scaled to one, Another way to think of this is the ratio of pedal revolutions to wheel revolutions. b.) Assuming 1.2 revolutions per second, compute the pedal revolutions per minute. b.) Pedaling Rate: c) Wheel Revolutions Circumference: Speed: 1.2 pedal rps (revolutions per second) 72 pedal rpm (revolutions per minute) wheel revolutions per second e) Coripute the wheel revolutions per second. If the gear ratio is 5 and the pedals go around once, this means the wheels will go around 5 times. 2.5 feet (so 1 complete revolution moves you this for fps (feet per second) mph (miles per hour) d.) c.) f.) Pedaling rate: mps (to go 30 mph) d.) Compute your speed in feet per second using the circumferer or of the tire and the wheel revolutions per second. e.) Compute you speed in mph using the ratio 3 fps: 2 mph. f.) Your speed (mph) is proportional to the revolctions per rond (ro) low fad do you have to pedaal (in nn) on this bike to travel a 30 mph? Enter a formule using the number 30 and a proportion with two of the numbers compaled above. check your answer by typing it into the Pedaling rate box! -) a.) Compute the gear ratio of the front gear to the back gear with the second quantity scaled to one. Another way to think of this is the ratio of pedal revolutions to wheel revolutions. b.) Assuming 1.2 revolutions per second, compute the pedal revolutions per minute. c.) Compute the wheel revolutions per second. If the gear ratio is 5 and the pedals go around once, this means the wheels will go around 5 times. this far d.) Compute your speed in feet per second using the circumference of the tire and the wheel revolutions per second. e.) Compute your speed in mph using the ratio 3 fps : 2 mph. f.) Your speed (mph) is proportional to the revolutions per second (rps). How fast do you have to pedal (in rps) on this bike to travel at 30 mph? Enter a formula using the number 30 and a proportion with two of the numbers computed above. Check your answer by typing it into the Pedaling Rate box! Pedaling Rate: Wheel Revolutions: Circumference: Speed: 1.2 pedal rps (revolutions per second) pedal rpm (revolutions per minute) wheel revolutions per second 2.5 feet (so 1 complete revolution moves you fps (feet per second) d.) Com mph (miles per hour) + tire and Pedaling rate: rps (to go 30 mph) e.) Comp --) Pedaling Rate: Wheel Revolutions: Circumference: Speed: 1.2 pedal rps (revolutions per second) pedal rpm (revolutions per minute) wheel revolutions per second c.) Con pedals 2.5 feet (so 1 complete revolution moves you this far) fps (feet per second) d.) Compute your mph (miles per hour) tire and the wheel Pedaling rate: rps (to go 30 mph) e.) Compute your s # Teeth in the Gear sprocket Pedals 36 a.) Back Wheel 12 qua Gear Ratio: 3:1 a.) rev 12 2 Use a cell reference or a single formula where appropriate in order to receive full credit. Do not copy and past 3 4 Do you know how bicycle gears work? Let's first consider a tricycle where the pedals are directly connected to the front tire. If you turn the pedals one revolution, then the front tire also turns one complete revolution. Thus the distance you move is related to how big the front tire is. Assuming you pedal at 1 revolution per 6 second, or 60 revolutions per minute (rpm), and the circumference of the front tire is 3 feet; then you will 5 7 8 9 move 3 feet per second (fps). Converting this to miles per hour (which we will discuss in the next chapter), 3 fps is approximately 2 mph... not very fast. To go faster you would have to increase your rpm by pedaling faster or increase the size of the front wheel, hence those goofy looking tricycles from 100 years ago. The 10 better way to go faster is to use gears: by putting a gear with 24 teeth up front (attached to the pedals) and a 11 gear with only 12 teeth in back (attached to the rear wheel), then every time you turn the pedals one 12 13 a complete revolution, the rear wheel will go around twice. The gear ratio of front to back is 24 teeth : 12 teeth or 2:1. This problem uses the ratio 36: 12 for the gear ratio, Pedals: Rear. 14 15 16 where the pedals are directly connected to re also turns one complete revolution. suming you pedal at 1 revolution per of the front tire is 3 feet; then you will ich we will discuss in the next chapter), 3 mave to increase your rpm by pedaling oking tricycles from 100 years ago. The eth up front (attached to the pedals) and a very time you turn the pedals one ratio of front to back is 24 teeth: 12 teeth als: Rear. Pedals #Teeth in the Gear sprocket 36 12 a.) Back Wheel Gear Ratio: 3:1 12 a.) Compute the gear ratio of the front gear to the back gear with the second quantity scaled to one. Another way to think of this is the ratio of pedal revolutions to wheel revolutions. b.) Assuming 1.2 revolutions per second, compute the pedal revolutions per minute. b.) Pedaling Rate: c.) Wheel Revolutions d.) Circumference: Speed: 1.2 pedal rps (revolutions per second) pedal rpm (revolutions per minute) wheel revolutions per second c) Compute the wheel revolutions per second. If the gear ratio is 5 and the pedals go around once, this means the wheels will go around 5 times. 2.5 feet (so 1 complete revolution moves you this far) fps (feet per second) mph (miles per hour) f.) Pedaling rate: rps (to go 30 mph) d.) Compute your speed in feet per second using the circumference of the tire and the wheel revolutions per second. e.) Compute your speed in mph using the ratio 3 fps: 2 mph. f.) Your speed (mph) is proportional to the revolutions per second (rps). How fast do you have to pedal (in rps) on this bike to travel at 30 mph? Enter a formula using the number 30 and a proportion with two of the numbers computed above. Check your answer by typing it into the Pedaling Rate box!