Create and use Mohr’s circles at A and B two points to determine principal stresses. The maximum principal stress with the desirable factor of safety must not be greater the allowable stress 24 ksi. Assume the geometric effect of stress concentration where the beam was attached to the wall is negligible. It is expected that the maximum stress could be applied at point A or B. Use your own factor of safety for the static loading condition.

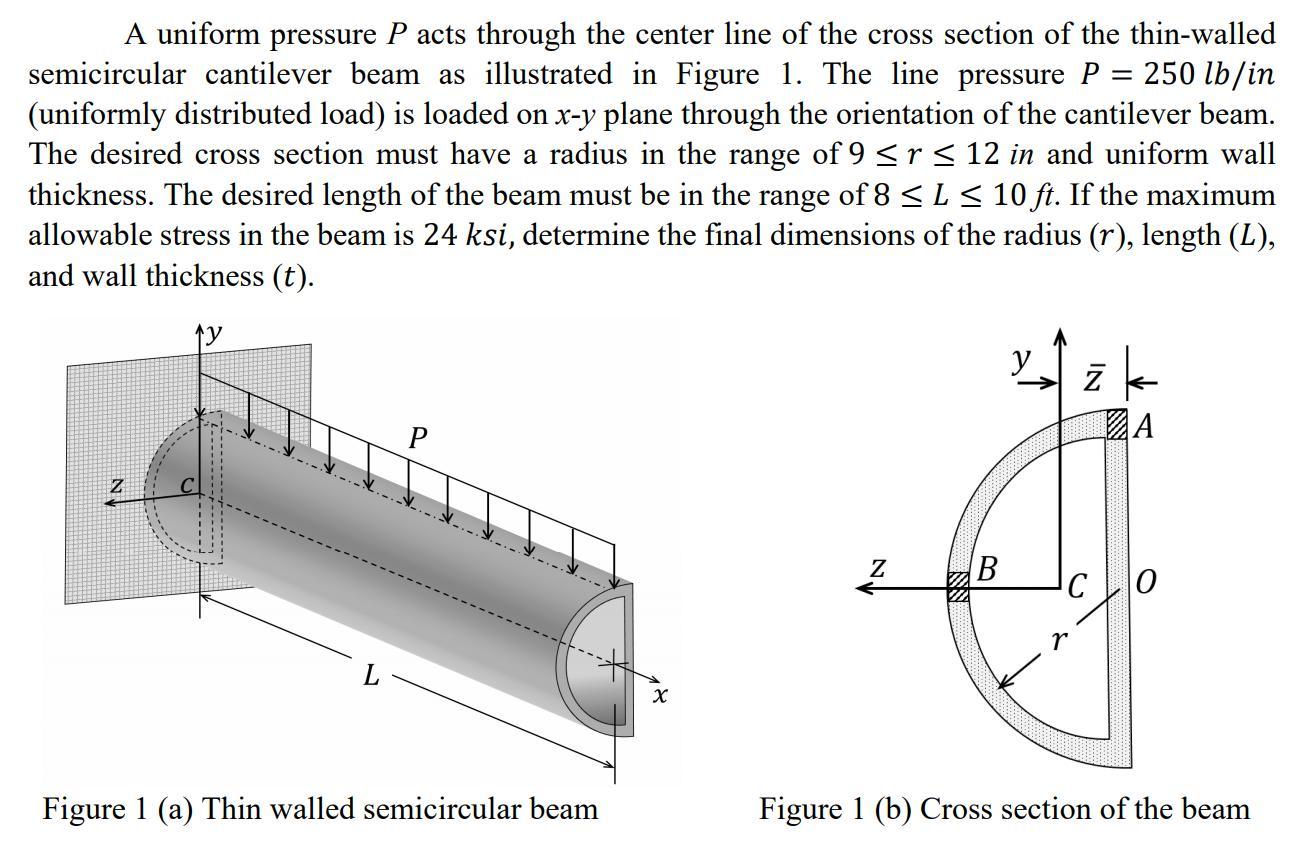
A uniform pressure P acts through the center line of the cross section of the thin-walled semicircular cantilever beam as illustrated in Figure 1. The line pressure P = 250 lb/in (uniformly distributed load) is loaded on x-y plane through the orientation of the cantilever beam. The desired cross section must have a radius in the range of 9 r 12 in and uniform wall thickness. The desired length of the beam must be in the range of 8 L 10 ft. If the maximum allowable stress in the beam is 24 ksi, determine the final dimensions of the radius (r), length (L), and wall thickness (t). P Figure 1 (a) Thin walled semicircular beam X Z NN B y IN r A C 0 Figure 1 (b) Cross section of the beam