Credit Risk Management
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
I HAVE MANAGED TO SOLVE IT BUT I A, NOT SO SURE REGARDING MY SOLUTIONS BUT YOU CAN FIX WHERE I WENT WRONG:


I AM STRUGGLING ESPECIALLY WITH Face value of debt and present value of debt) and i don't know which one to choose for 5000\
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
THESE NOTES WILL GUIDE YOU:

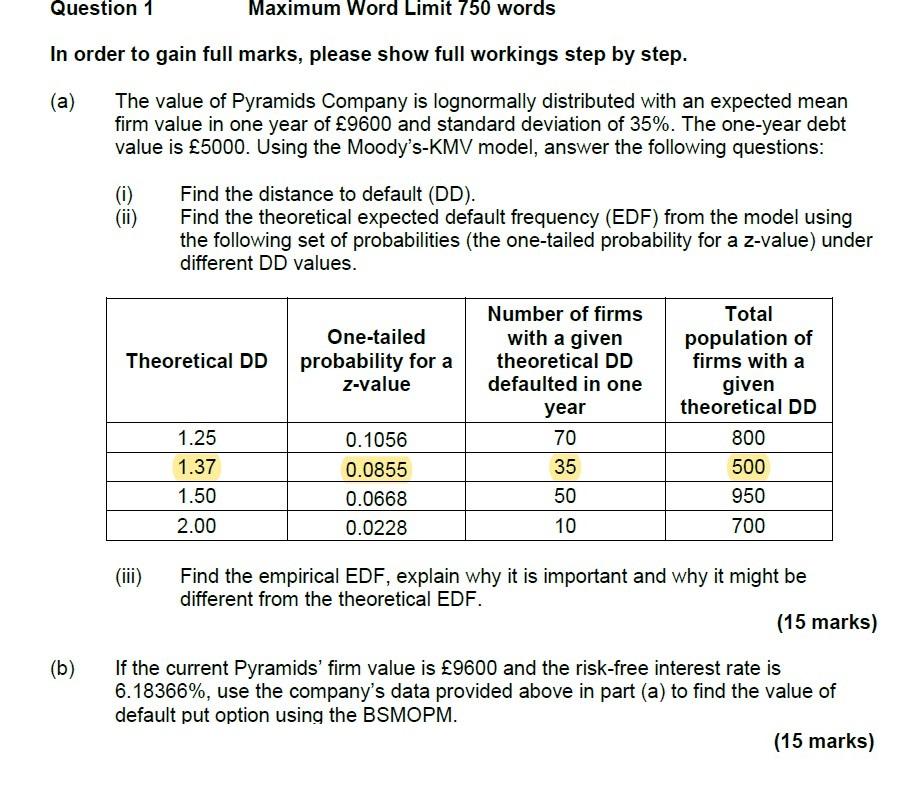
Question 1 Maximum Word Limit 750 words In order to gain full marks, please show full workings step by step. (a) The value of Pyramids Company is lognormally distributed with an expected mean firm value in one year of 9600 and standard deviation of 35%. The one-year debt value is 5000. Using the Moody's-KMV model, answer the following questions: (0) Find the distance to default (DD). Find the theoretical expected default frequency (EDF) from the model using the following set of probabilities (the one-tailed probability for a z-value) under different DD values. Number of firms with a given theoretical DD defaulted in one One-tailed probability for a z-value Theoretical DD Total population of firms with a given theoretical DD year 1.25 0.1056 70 800 1.37 0.0855 35 500 1.50 0.0668 50 950 2.00 0.0228 10 700 Find the empirical EDF, explain why it is important and why it might be different from the theoretical EDF. (15 marks) (b) If the current Pyramids' firm value is 9600 and the risk-free interest rate is 6.18366%, use the company's data provided above in part (a) to find the value of default put option using the BSMOPM. (15 marks) Question 1 (a) E(VT) = 9600, Ov = 35% and Dp = 5000 (1) E(VT)-DP The distance to default is calculated as: DD = E(VT)OV Where, Dp = Short-term debt + o Long-term debt 9600 - 5000 DD = E(VT) - DP EVTOV 9600 x 35% 4600 DD = 3360 DD = 1.37 The area under the curve from the normal distribution table for the DD value of 1.37 is 0.9147. There is 1-0.9145 = 0.0853 probability below the DD point. Therefore, the probability of default or the expected default frequency will be 0.0855, or 8.53% NORMSDIST (1.37) = 0.9147 1 - NORMSDIST (1.37) = 1 -0.9147 = 0.0853 (ii) One-tailed probability for a z-value under DD = 1.37 is 0.0855 or 8.55%, then the theoretical expected default frequency is 1.37. For, instance since the theorical EDF is 1.37, the number of firms is 35 over one year and then the total population is 500, then the empirical EDF would 35 / 500 = 0.07 (b) The formula to get the put potion using BSMOPM is Po = BreFT (1-N(dz)) - V.(1-N(d)) di OVT d2 = d7-OVT We have the following: Current value of the firm = 9 600 (V.) Volatility = 0 = 35 % Risk-free interest rate = 6.18366 % Maturity of the debt = T = 1 year Using in BSMOPM we have r= ln (1 + 0.0618366) = 0.060 Short-term debt = 5000 (Face value of the debt) Note that B7e0.06 = 5000e-0.06 = 4 708.82 (which is the present value of the debt. Leverage Ratio which is Debt / firm value = 4 708.82 / 9600 = 0.4905 = 49.050% di = 9600 0.252 (1) 0.35/(1) OVT di = 2.2102 da = d7-OVT d2 = 2.2102 -0.35V d2 = 1.8602 The values for d, and d, from the normal distribution table which are 0.9865 and 0.9686 respectively, then the equation will be written as: Po = Bre:FT (1-N(dz)) - V.(1-N(d)) Po = 4 708.82(1 - 0.9686) - 9600(1 - 0.9865) Po = 4 708.82 x 0.0314 - 9600 x 0.0135 Po = 18.26 Then, the present value of the risky bond will be Bo = ByeIT - P Bo = 4 708.82 -18.26 = 4 690.56 Take the following example of a firm that has: Leverage ratio = 0.7 Current value of the firm = 1000 Volatility = 30 per cent Risk-free interest rate = 5 per cent Maturity of the debt = 1 year* Based on the assumption we have made, the face value of the debt will be 735 and its present value 700 (hence leverage of 0.7). The continuously compounded interest rate (as used in BSMOPM) will be ln(1 + 0.05) = 0.04879 (i.e. 4.879 per cent continuously compounded). Given this information, the value of the put option can be calculated as: in E)+(r+ m) (7.15) B- di Vo In( Be-rt OVT = 1000 In 735 (1) 9)+(0.0487910:302) di = 1.3389 0.301 da = d; -ovi d2 = 1.3389 - 0.30/1 = 1.0389 The values for d, and d2 from the normal distribution table (given in Appendix 7.1 at the end of this module) are 0.9097 and 0.8506 respectively, so that Equation 7.13 of the BSMOPM then becomes: (7.16) Po = Bre-T (1 - N(dz)) - V.(1 - N(d)) Po = 700(0.1494) - 1000(0.0903) = 14.3 Based on Equation 7.1 or 7.12, the present value of the risky bond (Bo) will be: Bo = Bre-T PO = 700 14.3 = 685.67 Question 1 Maximum Word Limit 750 words In order to gain full marks, please show full workings step by step. (a) The value of Pyramids Company is lognormally distributed with an expected mean firm value in one year of 9600 and standard deviation of 35%. The one-year debt value is 5000. Using the Moody's-KMV model, answer the following questions: (0) Find the distance to default (DD). Find the theoretical expected default frequency (EDF) from the model using the following set of probabilities (the one-tailed probability for a z-value) under different DD values. Number of firms with a given theoretical DD defaulted in one One-tailed probability for a z-value Theoretical DD Total population of firms with a given theoretical DD year 1.25 0.1056 70 800 1.37 0.0855 35 500 1.50 0.0668 50 950 2.00 0.0228 10 700 Find the empirical EDF, explain why it is important and why it might be different from the theoretical EDF. (15 marks) (b) If the current Pyramids' firm value is 9600 and the risk-free interest rate is 6.18366%, use the company's data provided above in part (a) to find the value of default put option using the BSMOPM. (15 marks) Question 1 (a) E(VT) = 9600, Ov = 35% and Dp = 5000 (1) E(VT)-DP The distance to default is calculated as: DD = E(VT)OV Where, Dp = Short-term debt + o Long-term debt 9600 - 5000 DD = E(VT) - DP EVTOV 9600 x 35% 4600 DD = 3360 DD = 1.37 The area under the curve from the normal distribution table for the DD value of 1.37 is 0.9147. There is 1-0.9145 = 0.0853 probability below the DD point. Therefore, the probability of default or the expected default frequency will be 0.0855, or 8.53% NORMSDIST (1.37) = 0.9147 1 - NORMSDIST (1.37) = 1 -0.9147 = 0.0853 (ii) One-tailed probability for a z-value under DD = 1.37 is 0.0855 or 8.55%, then the theoretical expected default frequency is 1.37. For, instance since the theorical EDF is 1.37, the number of firms is 35 over one year and then the total population is 500, then the empirical EDF would 35 / 500 = 0.07 (b) The formula to get the put potion using BSMOPM is Po = BreFT (1-N(dz)) - V.(1-N(d)) di OVT d2 = d7-OVT We have the following: Current value of the firm = 9 600 (V.) Volatility = 0 = 35 % Risk-free interest rate = 6.18366 % Maturity of the debt = T = 1 year Using in BSMOPM we have r= ln (1 + 0.0618366) = 0.060 Short-term debt = 5000 (Face value of the debt) Note that B7e0.06 = 5000e-0.06 = 4 708.82 (which is the present value of the debt. Leverage Ratio which is Debt / firm value = 4 708.82 / 9600 = 0.4905 = 49.050% di = 9600 0.252 (1) 0.35/(1) OVT di = 2.2102 da = d7-OVT d2 = 2.2102 -0.35V d2 = 1.8602 The values for d, and d, from the normal distribution table which are 0.9865 and 0.9686 respectively, then the equation will be written as: Po = Bre:FT (1-N(dz)) - V.(1-N(d)) Po = 4 708.82(1 - 0.9686) - 9600(1 - 0.9865) Po = 4 708.82 x 0.0314 - 9600 x 0.0135 Po = 18.26 Then, the present value of the risky bond will be Bo = ByeIT - P Bo = 4 708.82 -18.26 = 4 690.56 Take the following example of a firm that has: Leverage ratio = 0.7 Current value of the firm = 1000 Volatility = 30 per cent Risk-free interest rate = 5 per cent Maturity of the debt = 1 year* Based on the assumption we have made, the face value of the debt will be 735 and its present value 700 (hence leverage of 0.7). The continuously compounded interest rate (as used in BSMOPM) will be ln(1 + 0.05) = 0.04879 (i.e. 4.879 per cent continuously compounded). Given this information, the value of the put option can be calculated as: in E)+(r+ m) (7.15) B- di Vo In( Be-rt OVT = 1000 In 735 (1) 9)+(0.0487910:302) di = 1.3389 0.301 da = d; -ovi d2 = 1.3389 - 0.30/1 = 1.0389 The values for d, and d2 from the normal distribution table (given in Appendix 7.1 at the end of this module) are 0.9097 and 0.8506 respectively, so that Equation 7.13 of the BSMOPM then becomes: (7.16) Po = Bre-T (1 - N(dz)) - V.(1 - N(d)) Po = 700(0.1494) - 1000(0.0903) = 14.3 Based on Equation 7.1 or 7.12, the present value of the risky bond (Bo) will be: Bo = Bre-T PO = 700 14.3 = 685.67










