(Cryptography: Arithmetic on Elliptic Curves)

List the points of the elliptic curve E: y 2 = x 3 2 (mod 7). Find the sum (3,2) + (5,5) on E and the sum (3,2) + (3,2) on E. Hint: E has seven points, including (,).

Reference

|A| = the number of elements in set A.

(n) = |{ a Z⁺_n : gcd(a, n) = 1 }|.

Eulers Theorem: For each n > 1 and a Z_n : a⁽ⁿ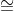⁾ 1 (mod n).

g is a primitive element of Z_n iff { g¹ , g² , . . . , g⁽ⁿ⁾ } = Z_n .

Suppose g is a primitive element of Z_n . For a Z_n, the discrete log of a to the base g mod p (written: dlog_g (a)) is the solution for x of: g^x 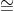a (mod n), i.e., g ^dlog_g(a) 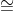a (mod n).

Definition. Suppose a, n Z with n > 1 and a 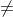0. (a) a is a quadratic residue mod n when x² a (mod n) has a solution, otherwise a is a nonresidue. (b) QR_n = the quadratic residues mod n. (c) Suppose n is the product of two distinct odd primes p and q. 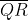n = { a : ( ) = 1 = ( ) } = the pseudo-residues mod n.