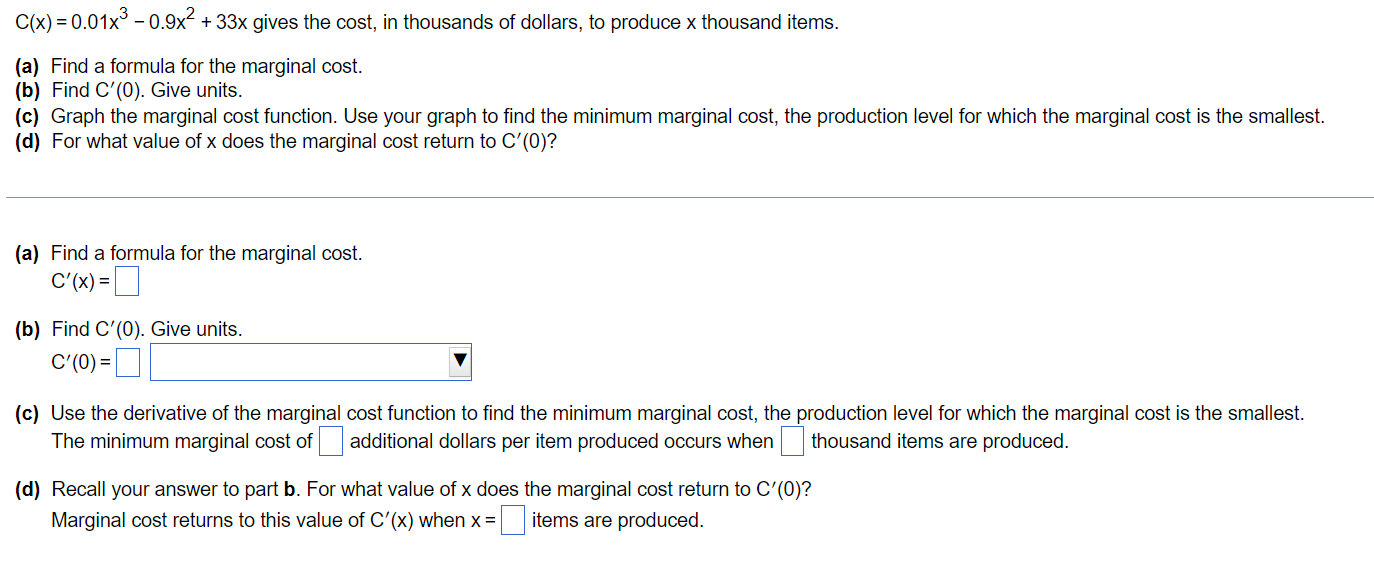
C(x) = 0.01x-0.9x + 33x gives the cost, in thousands of dollars, to produce x thousand items. (a) Find a formula for the marginal cost. (b) Find C'(0), Give units. (c) Graph the marginal cost function. Use your graph to find the minimum marginal cost, the production level for which the marginal cost is the smallest. (d) For what value of x does the marginal cost return to C'(0)? (a) Find a formula for the marginal cost. C'(x) = (b) Find C'(0). Give units. C'(0)= (c) Use the derivative of the marginal cost function to find the minimum marginal cost, the production level for which the marginal cost is the smallest. The minimum marginal cost of additional dollars per item produced occurs when thousand items are produced. (d) Recall your answer to part b. For what value of x does the marginal cost return to C'(0)? Marginal cost returns to this value of C'(x) when x= items are produced.