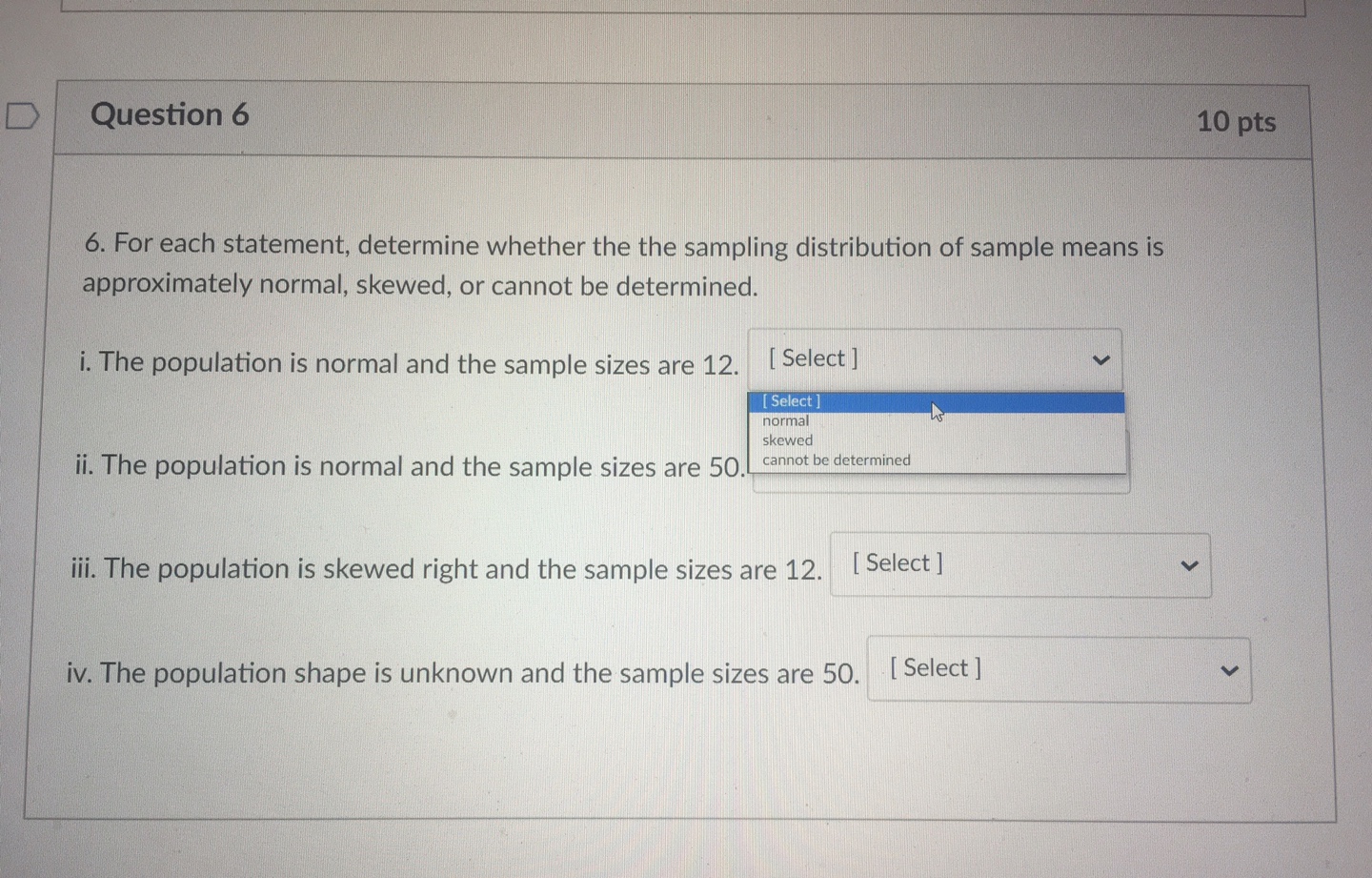
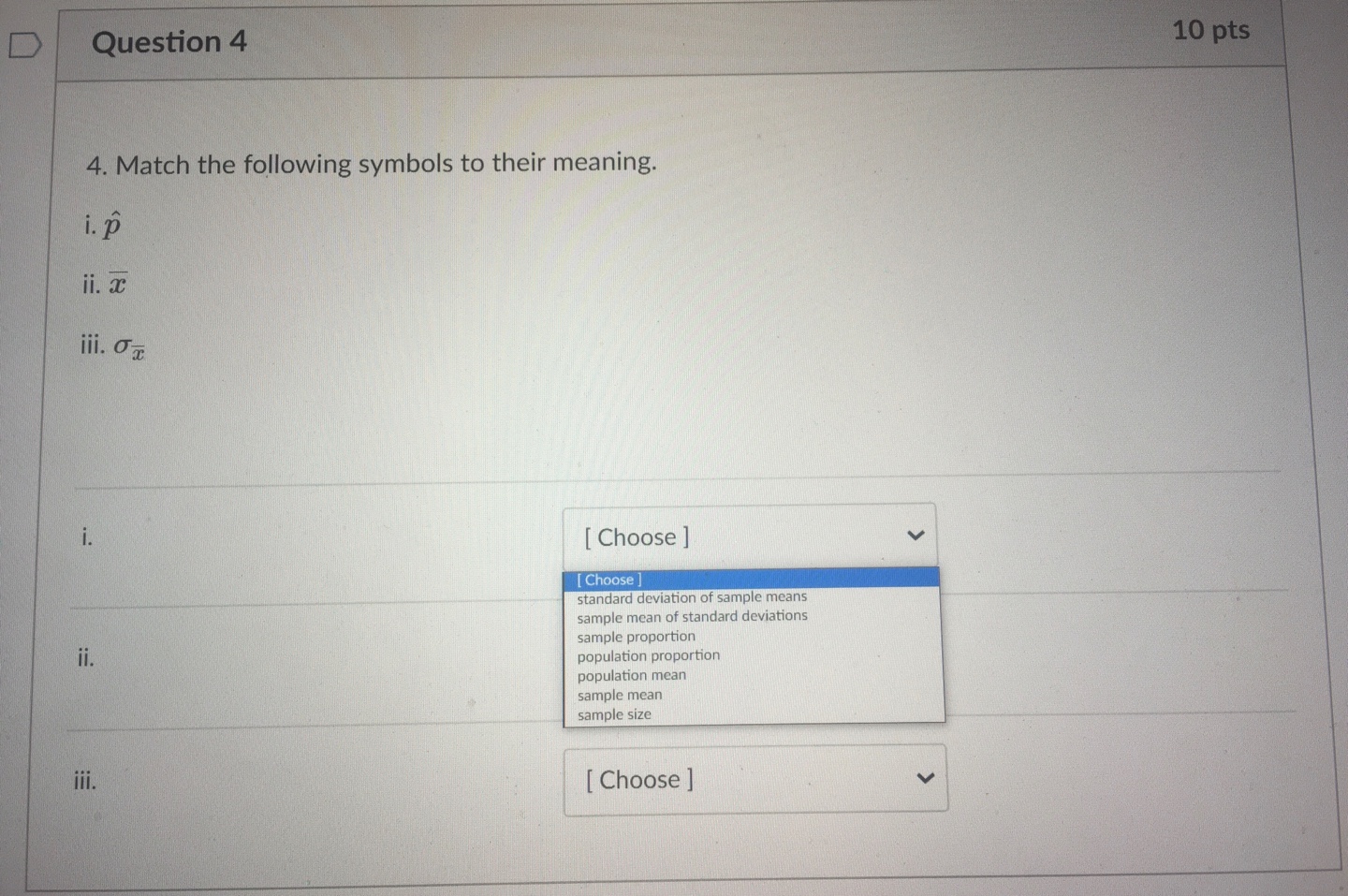
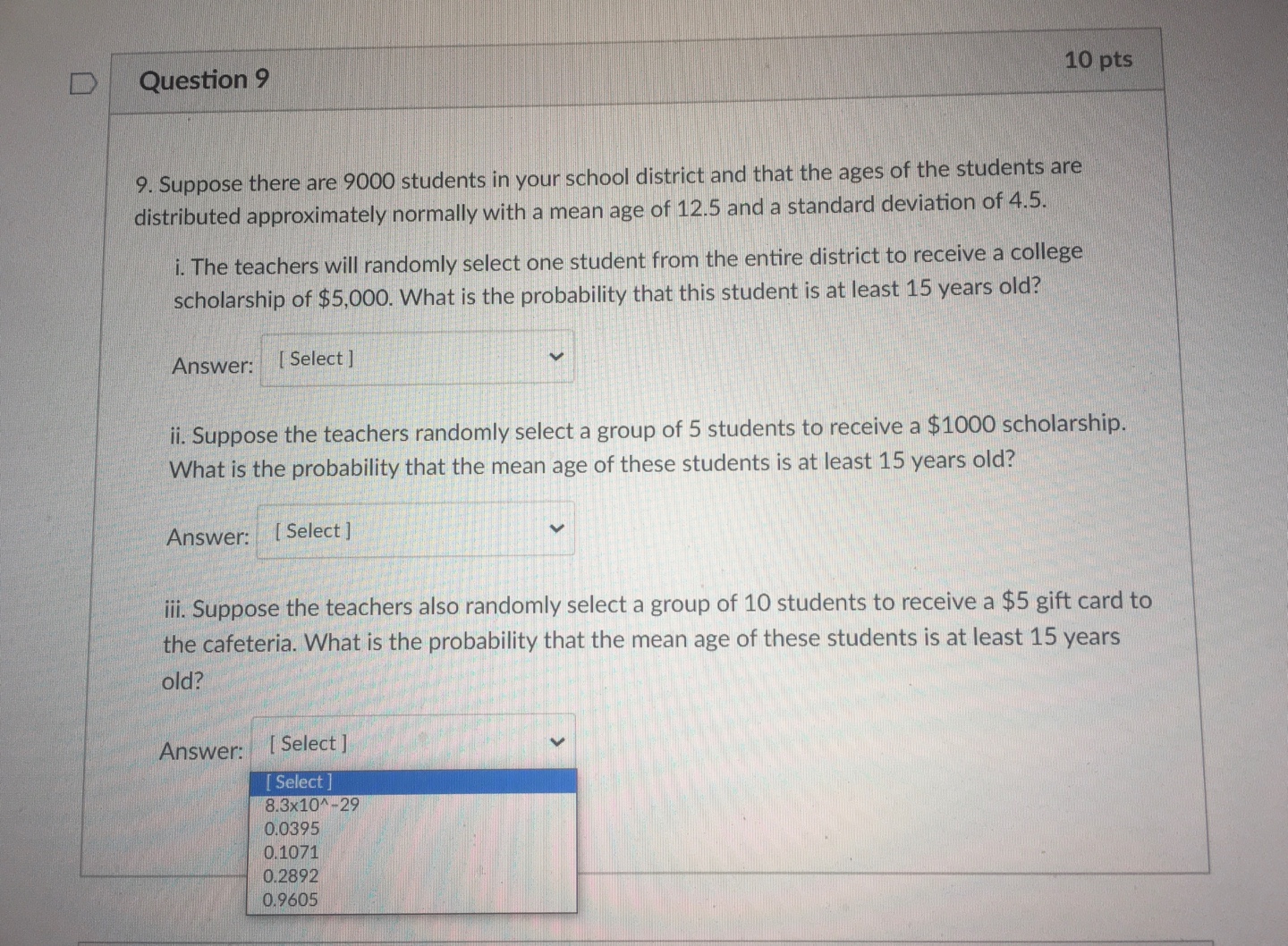
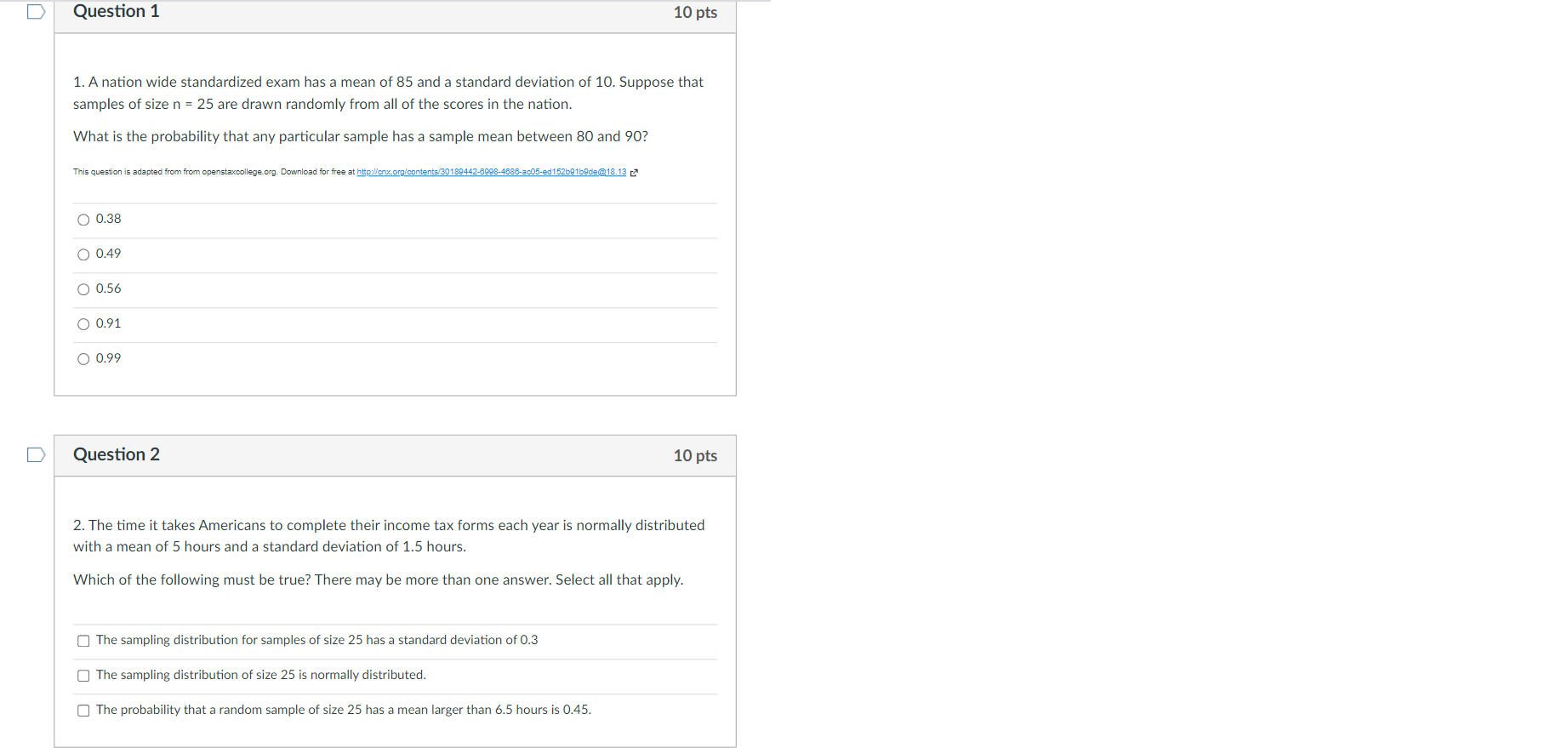

D Question 8 10 pts 8. Suppose a law firm has 1,000 across the country, divided equally into teams of 20 workers in each of the 50 states in the United States. The distributions of salaries of these thousand workers has a mean of $65,000 and a standard deviation of $4,500. i. If we randomly select one of the 1,000 workers, what is the probability that person would have a salary between $55,000 and $70,000? Answer: [ Select ] ii. Consider each team of 20 as a random sample. If we look at any one particular team, what is the probability that the mean salary of this team is between $55,000 and $70,000? Answer: [ Select ] [ Select 0.9999 0.9191 0.8536 0.6835 0.3865Question 6 10 pts 6. For each statement, determine whether the the sampling distribution of sample means is approximately normal, skewed, or cannot be determined. i. The population is normal and the sample sizes are 12. [ Select ] Select] normal skewed ii. The population is normal and the sample sizes are 50. cannot be determined iii. The population is skewed right and the sample sizes are 12. [Select ] iv. The population shape is unknown and the sample sizes are 50. [ Select ]D Question 4 10 pts 4. Match the following symbols to their meaning. i. p ii. ac iii. ox [ Choose ] [ Choose standard deviation of sample means sample mean of standard deviations ii. sample proportion population proportion population mean sample mean sample size jii. [ Choose ]D Question 9 10 pts 9. Suppose there are 9000 students in your school district and that the ages of the students are distributed approximately normally with a mean age of 12.5 and a standard deviation of 4.5. i. The teachers will randomly select one student from the entire district to receive a college scholarship of $5,000. What is the probability that this student is at least 15 years old? Answer: [ Select ] ii. Suppose the teachers randomly select a group of 5 students to receive a $1000 scholarship. What is the probability that the mean age of these students is at least 15 years old? Answer: [Select ] iii. Suppose the teachers also randomly select a group of 10 students to receive a $5 gift card to the cafeteria. What is the probability that the mean age of these students is at least 15 years old? Answer: [Select ] [ Select ] 8.3x10^-29 0.0395 0.1071 0.2892 0.9605D Question 1 10 pts 1. A nation wide standardized exam has a mean of 85 and a standard deviation of 10. Suppose that samples of size n = 25 are drawn randomly from all of the scores in the nation. What is the probability that any particular sample has a sample mean between 80 and 90? This question is adapted from from openstaxcollege. org. Download for free at http:/cox.org/contents/30180442-8098-4886-ac05-ed152b@1b0de@18.13p O 0.38 O 0.49 O 0.56 O 0.91 O 0.99 D Question 2 10 pts 2. The time it takes Americans to complete their income tax forms each year is normally distributed with a mean of 5 hours and a standard deviation of 1.5 hours. Which of the following must be true? There may be more than one answer. Select all that apply. The sampling distribution for samples of size 25 has a standard deviation of 0.3 The sampling distribution of size 25 is normally distributed. The probability that a random sample of size 25 has a mean larger than 6.5 hours is 0.45.Question 3 10 pts 3. The citizens of Footville, Wisconsin aren't too concerned with dental care (maybe they're more concerned with foot care). Only 65% of the citizens get a dental check up at least twice a year as recommended. Random samples of 50 residents are surveyed and the sample proportion is computed. What are the mean and standard deviation of the sampling distribution of the sample proportion? O 0.65, 0.067 O 0.65, 0.092 Question 5 10 pts 5. A large unknown distribution has a standard deviation of 26. The statisticians want to create a sampling distribution of sample means with a standard deviation less than 3. To make it as easy as possible to generate, which is the smallest sample size the statisticans should use? 049 053 059 075 Question 7 10 pts 7. Suppose that your stats teacher claims the amount of time children can look at a marshmallow before eating it is approximately normally distributed with a mean of 12.4 seconds and a standard deviation of 3 seconds. You decide to try the experiment on 10 random children and nd they were able to resist eating the marshmallow for an average of 15 seconds. Would you conclude that your teacher is probably correct by claiming an average of 12.4 seconds? Why or why not? Q Probably correct because the teacher's info would suggest about 30.1% of samples of size 10 could have a mean of 15 or higher. 0 Probably incorrect because the teacher's info would suggest about 0.3% of samples of size 10 could have a mean of 15 or higher. 0 Probably correct because the teacher's info would suggest about 30.1% of samples of size 10 could have a 10. Answer each question in the box below. 3) Identify all possible samples of size n = 2 that can be obtained from rolling a six-sided die. For example, you roll the die twice and get 4 the rst time and 6 the second time, so (4, 6) is one possible sample of size n = 2. b) Find the mean of each sample. For example, the sample described above, (4, 6) has a mean of 5. Then, show that the mean of the sampling distribution of the means is equal to the mean of the population {1,23,45,63}. c) What is the standard deviation of the population? Explain how to nd the standard deviation of the distribution of the sample means based on the standard deviation of the population























