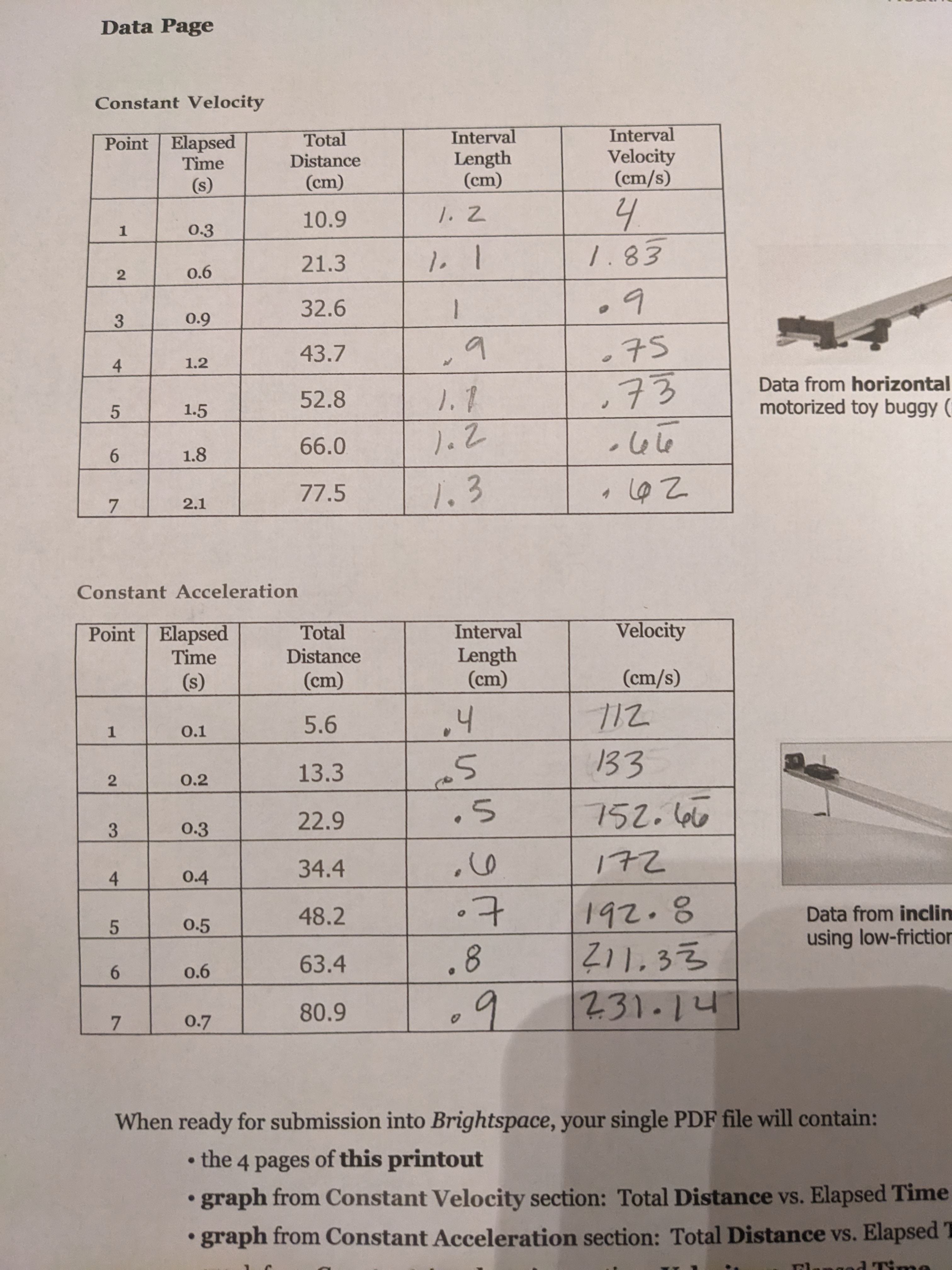
Data Page Constant Velocity Point Elapsed Total Interval Interval Time Distance Length Velocity (s) (cm) (cm) (cm/s) 1 0.3 10.9 1. Z 4 2 0.6 21.3 1. 1 1. 83 3 0.9 32.6 1 - 9 4 1.2 43.7 . 75 5 1.5 52.8 1. 8 73 Data from horizontal motorized toy buggy 6 1.8 66.0 1 . 2 le le 2.1 77.5 1.3 Constant Acceleration Point Elapsed Total Interval Velocity Time Distance Length (s) (cm) (cm) (cm/s) 0.1 5.6 . 4 712 2 0.2 13.3 6 5 133 3 0.3 22.9 . 5 752. 46 4 0.4 34.4 . CO 172 5 0.5 48.2 7 192 . 8 Data from inclir using low-frictio 6 0.6 63.4 . 8 21 1. 3 3 0.7 80.9 . 9 231. 14 When ready for submission into Brightspace, your single PDF file will contain: . the 4 pages of this printout graph from Constant Velocity section: Total Distance vs. Elapsed Time . graph from Constant Acceleration section: Total Distance vs. ElapsedKinematics Objective The general equation relating distance x and time t in this case is (2) In this experiment you will analyze motion graphi- * = xo + vol+ - at2 cally. and is the equation of a parabola. Apparatus Dynamics track, Table clamp, Steel rod, Track clamp, Constant speed buggy, Low-friction cart, Spark timer, Clamp, Spark tape, Masking tape, Meter stick. Background Kinematics is the study of motion, and one of the best tools for this purpose is graphs. Consider an object moving with a constant velocity (speed). This means that the object always travels X is still the initial position of the object; v. is its the same distance in a given amount of time. initial velocity and a the acceleration. The general equation relating distance x and time t The slope still represents the velocity of the object but in this case is here it is not constant - it is increasing. As a matter of fact the velocity is increasing uniformly with time. X = Xo + vt (1) The equation relating velocity and time in this case is and is the equation of a straight line. V = V. + at (3) and is another straight line. X Ax At V AV At x is the y-intercept and is the initial position of the object at t = o; the slope v is the velocity. t Ax distance slope = At = velocity time Here, vo is the y-intercept and the slope a is the ac- celeration. Thus, for any object moving with a constant velocity a graph of distance vs. time will always be straight Av velocity line whose slope is the velocity. slope = At = acceleration time Now consider an object moving with a constant pos- Thus, for any object moving with a constant accel- itive acceleration. This means that the object always eration, a graph of velocity vs. time will always be travels more and more distance in a given amount of straight line whose slope is the acceleration. time.Procedure Constant Velocity * To do in the Lab * The remainder of this section can be completed at home.** 1. The dynamics track should have a spark timer 8. Calculate the interval velocity by dividing each of clamped at one end and an end stop mounted at the interval lengths by the time it took through the other to stop the motion of the carts. Make each (0.3s). sure the track itself is relatively level. 1st Graph 2. Tear off a piece of spark tape as long as the track. 9 Graph total distance vs. elapsed time with the 12 pts Thread it through the back of the timer (shiny data. Draw the straight line of best fit over your side up) and attach it to the constant speed points and calculate the slope of the line. buggy at the same height it leaves the timer as 10. Answer the questions below. shown below. Questions 1. How do the interval lengths compare? Are they constant, increasing, or decreasing? 6 Is this what you expected? Why or why not? 2. How do the interval velocities compare? Are you confident that the buggy was moving with a constant velocity? Calculate the average interval velocity. 3. What is the slope of the line on your graph (don't 7 forget units!), and what does it represent? How does it compare to the average interval velocity? Would you expect them to be the same? Why or why not? 3. Set the timer to 10Hz via the switch on top. 4. When you are ready to make a run, turn on the buggy and then immediately turn on the timer Constant Acceleration * To do in the Lab * (you want minimal delay between the two). When the buggy hits the end stop pick it up and 1. Set the timer to 60Hz. turn it off; turn off the timer. 2. Clamp the table clamp at the side of the table 5. Remove the tape from the buggy and timer and and attach the vertical rod. Raise the timer end lay it on the table. Mark the first clear dot made of the track and attach it to the vertical rod with on the tape as the starting point (t = 0); now the track clamp (you want the raised end of the circle every third dot after this until you reach the track to be about 25cm above the table). You end of the tape. do not need to remove the track supports - just loosen the bolts on each and slide them to the raised end. This is shown below. 6. Measure the total distance from the starting point to each of your circled dots and record these 3. Tear off a piece of spark tape as long as the track. distances on the Data Page next to the corre- Thread it through the back of the timer and at- sponding times. (The timer is set to 10Hz which tach it to the low-friction cart; you will need to means 10 dots per second. Every third dot means hold the cart in front of the timer. the time increases in 0.3s increments). 7. Calculate the length of each interval, or the distance from one point to the next. The first is from Point 1 back to the starting point; the next from Point 2 back to Point 1, etc. 24. When you are ready to make a run, release the cart and turn on the timer at the same time. When the cart hits the end, turn off the timer. Questions 5. Remove the tape from the cart and timer, and lay it on the table. Mark the first clear dot on 1. How do the interval lengths compare? the tape as the starting point (t=0).; now circle Are they constant, increasing, or decreasing? every sixth dot after this, until you reach the Is this what you expected? end of the tape. Why or why not? 6. Measure the total distance from the starting point to each of your circled dots and 2. What happens to the velocity as time increases? record these distances on the Data Page. (The Is this what you expected? timer is set to 60Hz which means 60 dots per Why or why not? second. Every sixth dot means the time increases in 0.is increments). 3. What is the slope of the line on your velocity vs. time graph, and what does it represent? * The remainder of this section can be completed at home.** 7. Calculate the length of each interval. 8. Calculating the interval velocity does not make sense here, as the velocity of the cart is continuously increasing However, you can calculate the velocity at each point with velocity = 2 X total distance elapsed time The reason for the 2 in the equation above is that the velocity at each point should be about double what the average velocity is since vo = 0; remember average velocity is just total distance over total time. 9. Graph total distance vs. elapsed time with the 2nd Graph data. This data is non-linear, so freehand a 12 pts smooth curve over your points. 10 Graph velocity vs. elapsed time with the data. 3rd Graph Draw the straight line of best-fit over your 12 pts points, and calculate the slope of your line