Data Science Python 3.0 problem:

Let X the leading digit of a randomly selected number from a large accounting ledger. For example, if we randomly draw the number $20,695, then X = 2. People who make up numbers to commit accounting fraud tend to give X a (discrete) uniform distribution, i.e, 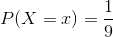. However, there is empirical evidence that suggests that naturally occurring numbers (e g, numbers in a non-fraudulent accounting ledgers) have leading digits that do not follow a uniform distribution. Instead, they follow a distribution defined by the following probability mass function .

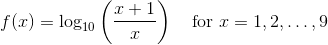Part A: Write a function pmf natural that implements f(x). Your function should take in an integer x and retum 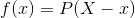. Use your function to argue that f(x) is a well-defined probability mass function

Python 3.0 :

def pmf_natural(x): return 1.0

Part B: Use the function you wrote above to make stacked bar plots describing the pmf of the natally occurring numbers as well as the discrete uniform distribution. Make sure that the x- and y- limits on your plots are the same so that the two distributions are easy to compare.

Part C: Write a function cdf_natural that implements the cumulative distribution function 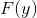for 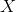and use it to compute the probability that the leading digit in a number is at most 4 and at most 5.

Python 3.0:

def cdf_natural(y) :

return 1.0

Part D: The data in tax_data.txt contains the taxable income for individuals in 1978. Use Pandas and the information from Parts A-D to determine whether or not the dataset is likely fraudulent. In addition to code and any graphical summaries make sure to clearly justify your conclusion in words.

tax_data.txt can be found here:

https://raw.githubusercontent.com/dblarremore/csci3022/master/homework/homework3/tax_data.txt

Let X the leading digit of a randomly selected number from a large accounting ledger. For example, if we randomly draw the number 520,695, then X 2. People who maka up numbers to commit accounting fraud tend to give X a (discrete) uniform distribution, i.e, PXxorxe ..,9). However, there is empirical evidence that suggests that naturally occurring numbers (e g, numbers in a non-fraudulent accounting ledgers) have leading digits that do not follow a uniform distribution. Instead, they follow a distribution defined by the following probability mass function f(x) = log10 (-x for x = 1,2 ,9 Part A: Write a function pmf natural that implements f(x). Your function should take in an integer x and retum f(x) Px- x). Use your function to argue that f(x) is a well-defined probability mass function det pat natural(x) return 1.0 Part B. Use the function you wrote above to make stacked bar plots describing the pmf of the natally occurring numbers as well as the discrete uniform distribution. Make sure that thexand y-limits on your plots are the same so that the two distributions are easy to compare Part C. Write a function fatural that implements the cumulative distribution function F(y) for X and use it to compute the probability that the leading digit in a number is at most 4 and at most 5 def odr natural v return 1.0 Part D. The data in tax_data.txt contains the taxable income for individuals in 1978. Use Pandas and the information from Parts A-D to determine whether or not the dataset is likely fraudulent. In addition to code and any graphical summaries make sure to clearly justify your conclusion in words. Let X the leading digit of a randomly selected number from a large accounting ledger. For example, if we randomly draw the number 520,695, then X 2. People who maka up numbers to commit accounting fraud tend to give X a (discrete) uniform distribution, i.e, PXxorxe ..,9). However, there is empirical evidence that suggests that naturally occurring numbers (e g, numbers in a non-fraudulent accounting ledgers) have leading digits that do not follow a uniform distribution. Instead, they follow a distribution defined by the following probability mass function f(x) = log10 (-x for x = 1,2 ,9 Part A: Write a function pmf natural that implements f(x). Your function should take in an integer x and retum f(x) Px- x). Use your function to argue that f(x) is a well-defined probability mass function det pat natural(x) return 1.0 Part B. Use the function you wrote above to make stacked bar plots describing the pmf of the natally occurring numbers as well as the discrete uniform distribution. Make sure that thexand y-limits on your plots are the same so that the two distributions are easy to compare Part C. Write a function fatural that implements the cumulative distribution function F(y) for X and use it to compute the probability that the leading digit in a number is at most 4 and at most 5 def odr natural v return 1.0 Part D. The data in tax_data.txt contains the taxable income for individuals in 1978. Use Pandas and the information from Parts A-D to determine whether or not the dataset is likely fraudulent. In addition to code and any graphical summaries make sure to clearly justify your conclusion in words