Dear tutor,
Please answer the quiz as fast as you can as I need to know the answer right now. No need for an explanation, just answers should be fine.
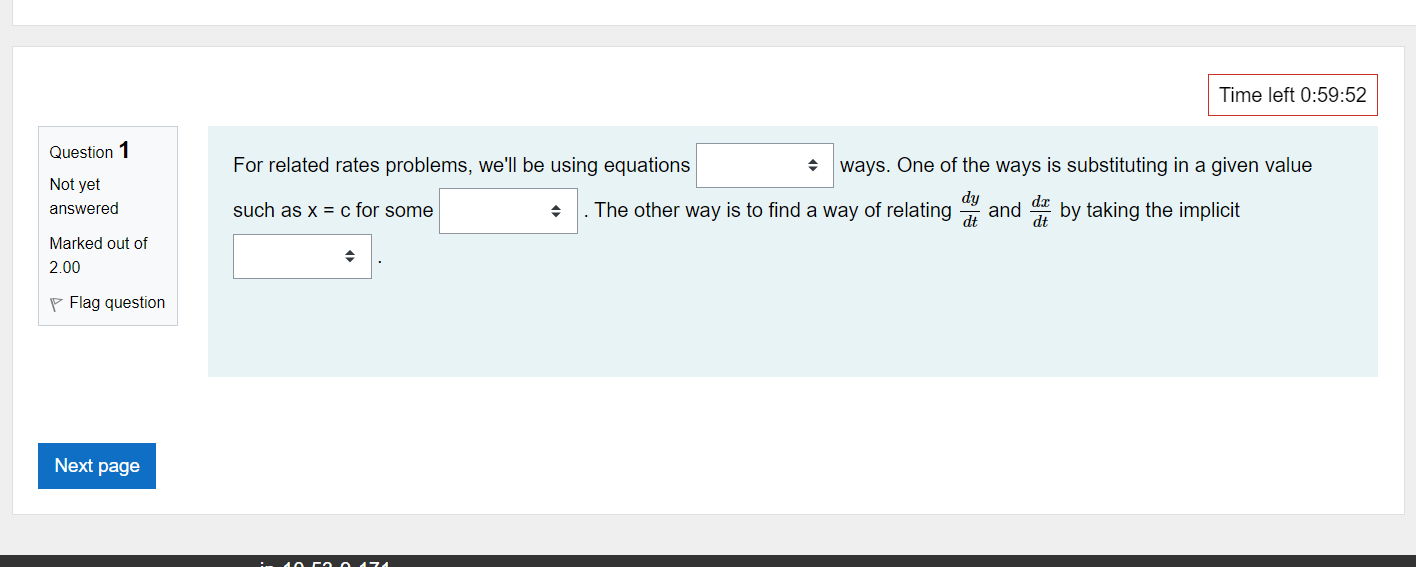
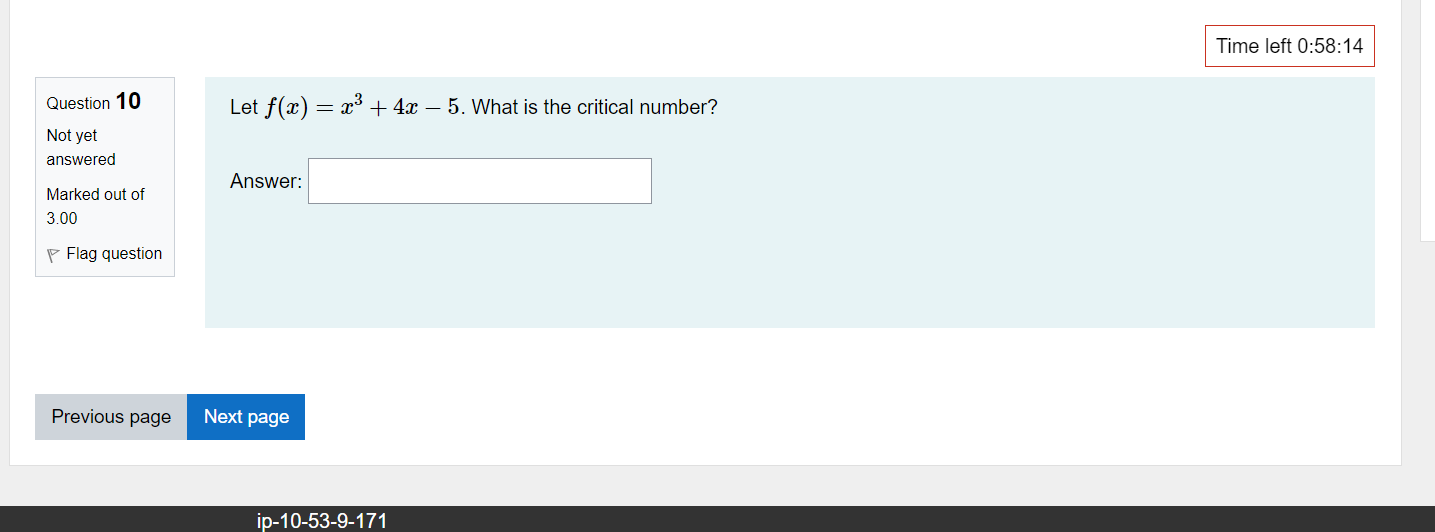
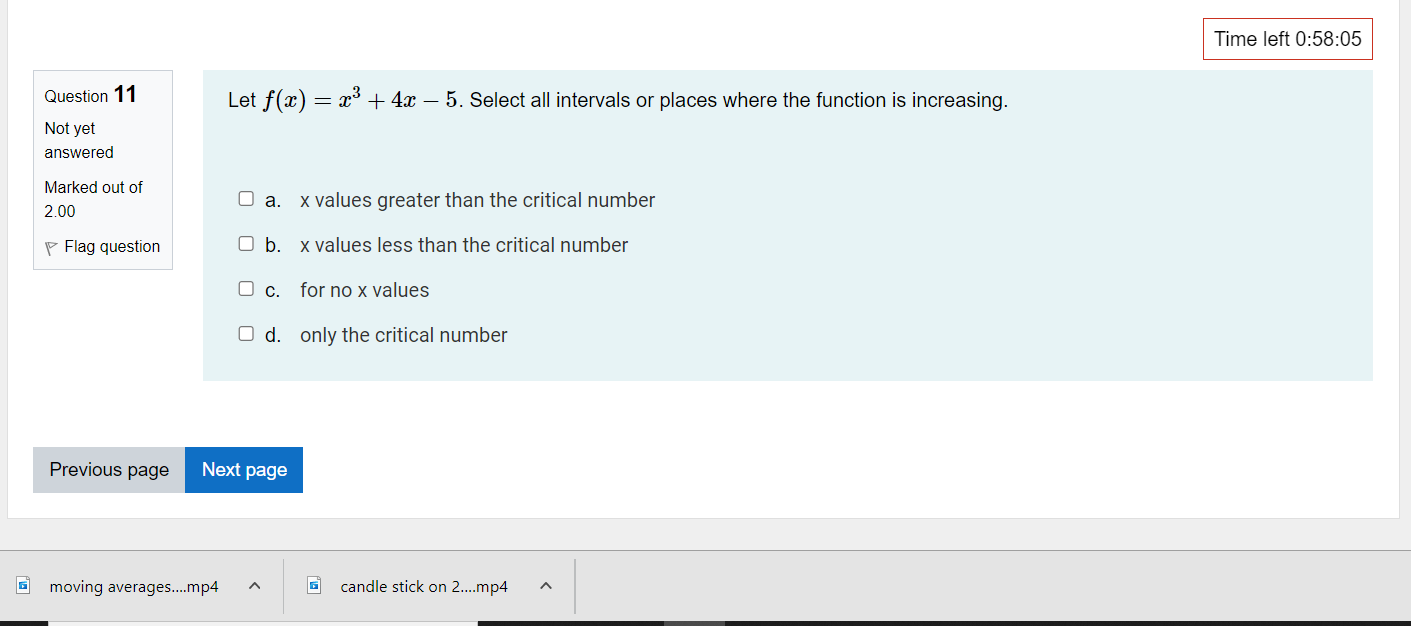
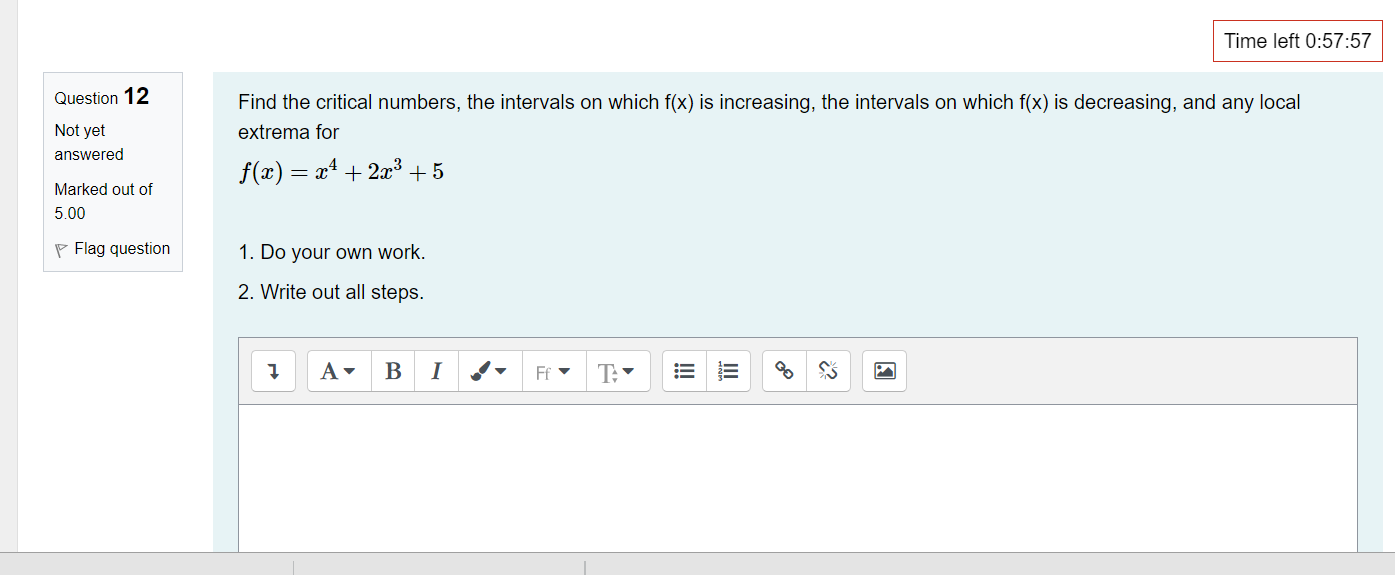
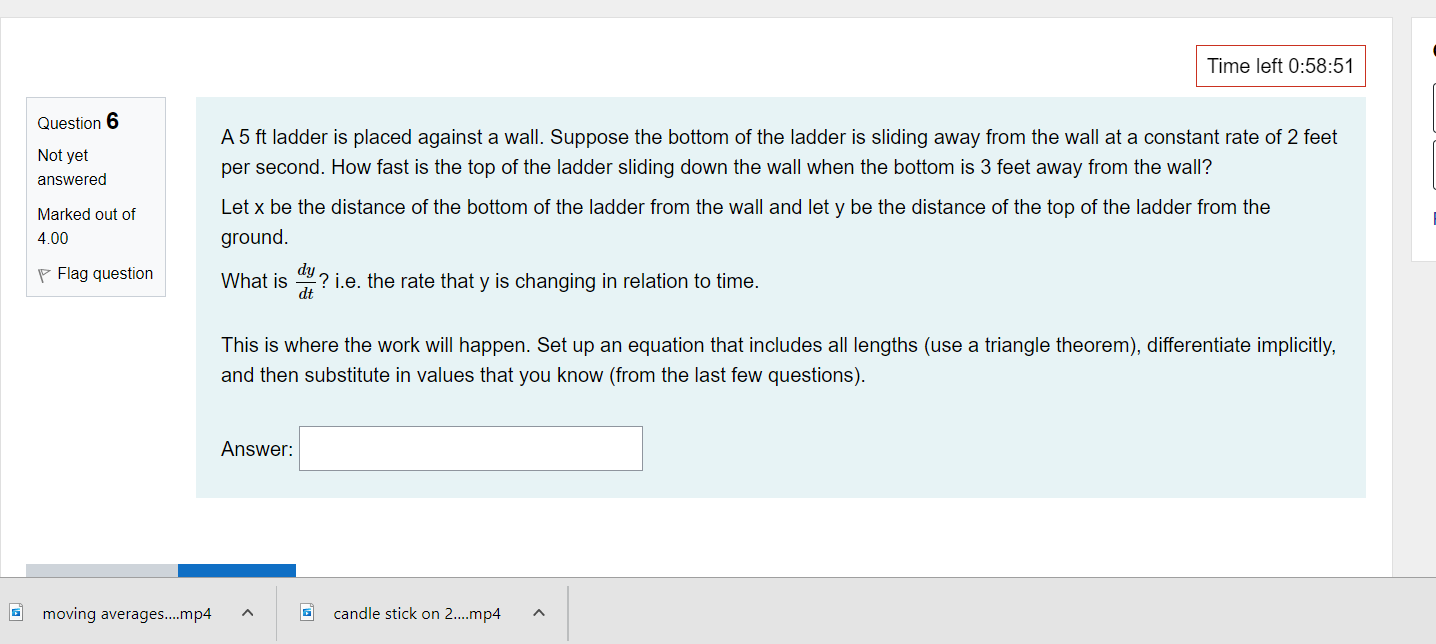
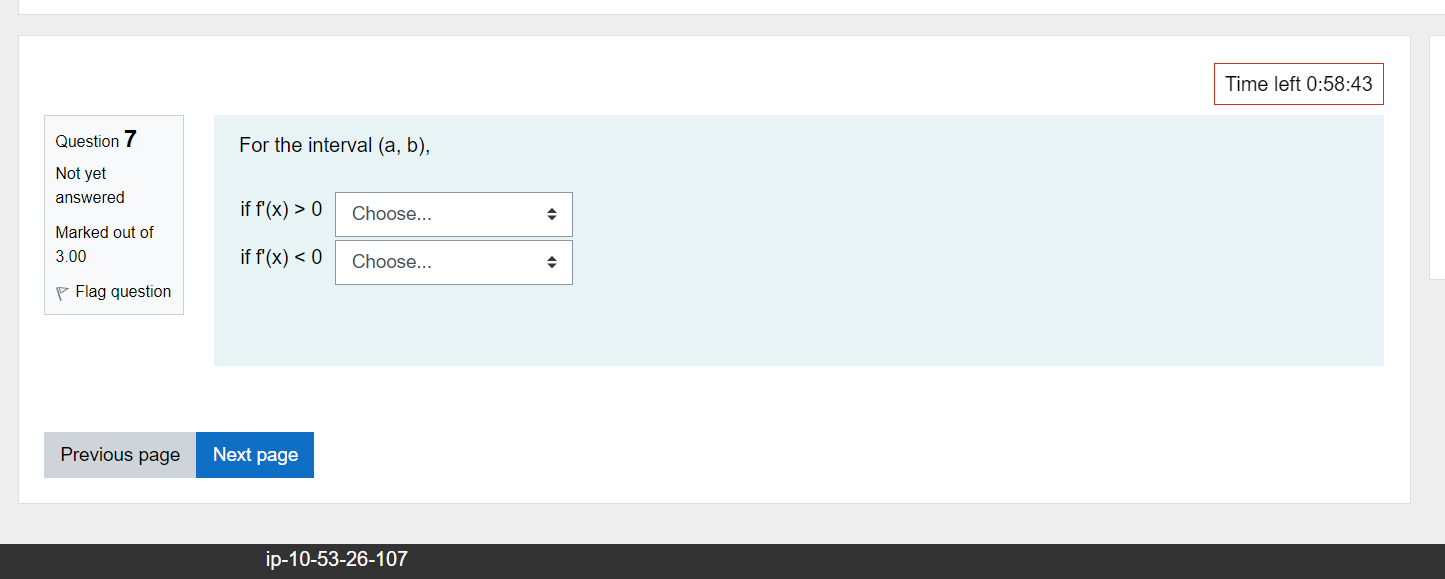
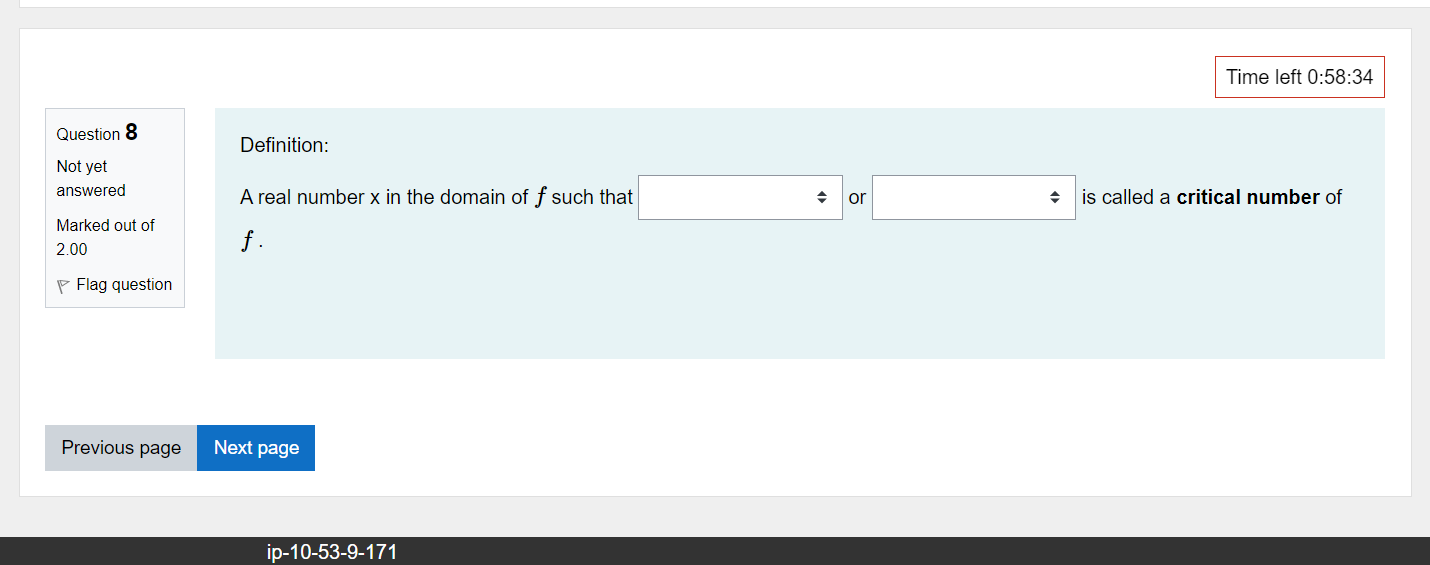
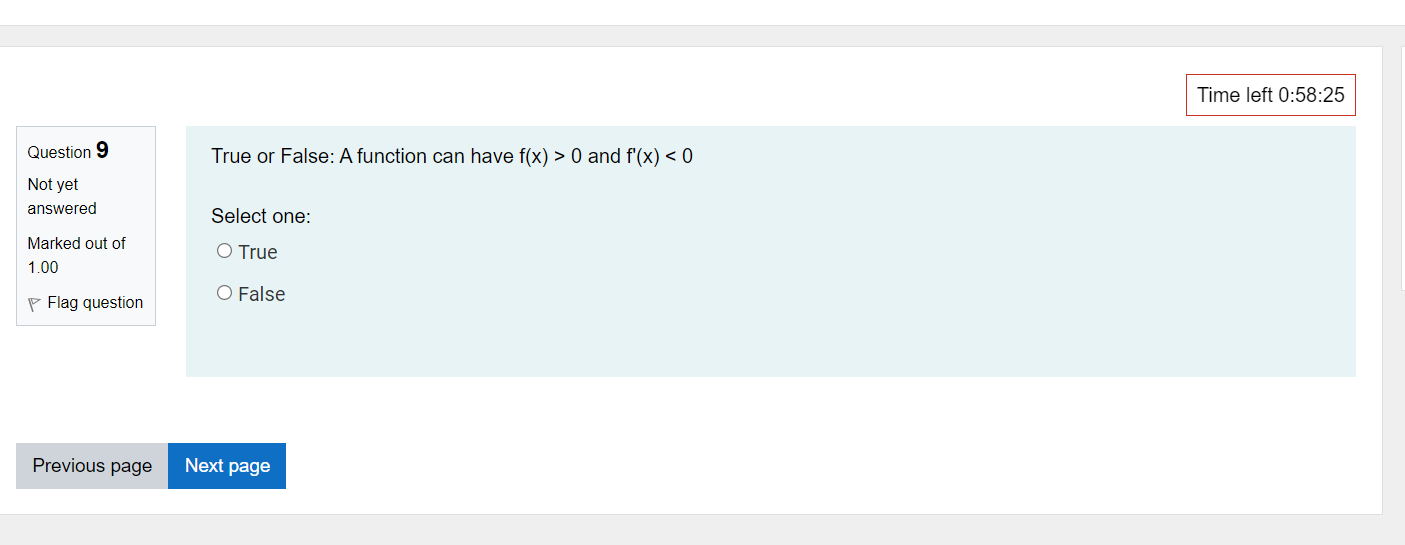
Time left 0:59:52 Question 1 For related rates problems, we'll be using equations ways. One of the ways is substituting in a given value Not yet answered such as x = c for some + The other way is to find a way of relating - and " by taking the implicit Marked out of 2.00 Flag question Next page\fQUBStion 11 Let m) : 2:3 + 4:1: 5. Select all intervals or places where the function is increasing. Not yet answered Marked out of 2 00 v Flag question C] b. x values less than the critical number C] c. for no x values C] C]. only the critical number C] a. x values greater than the critical number 'I'Ime left 0:58:05 a moving averages....mp4 A ' a candle stick on 2....mp4 A Question 1 2 Not yet answered Marked out of 5 00 P Flag question Time left 0:57:57 Find the critical numbers, the intervals on which f(x) is increasing, the intervals on which f(x) is decreasing, and any local extrema for f(.'.t) =:l:4 +2933+ 5 1. Do your own work. 2. Write out all steps. 1 AvBIah FE"T:' 5525 0995 IZI Question 2 Not yet answered Marked out of 2.00 V Flag question Time left 0:59:33 A 5 ft ladder is placed against a wall. Suppose the bottom ot the ladder is sliding away trom the wall at a constant rate 012 feet per second. How fast is the top of the ladder sliding down the wall when the bottom is 3 feet away from the wall? We note that the ladder is a c length, but the the top of the ladder will s rate that the bottom of the ladder is moving away from the wall. You can reference the animation below for this next part of the question: https:webspace.ship.edu/msrenault/GeoGebraCalculuslderivativeiappirrifallingiladder.html move down the wall at the Assume the ladder slides along the floor at a constant rate. The speed of the ladder on the wall as it moves down will be fastest at the c E moving averages....mp4 A a candle stick on 2....mp4 A Time left 0:59:22 t' 3 Ques Ion A 5 ft ladder is placed against a wall. Suppose the bottom of the ladder is sliding away from the wall at a constant rate of 2 feet ::;v::lred per second. How fast is the top of the ladder sliding down the wall when the bottom is 3 feet away from the wall? Marked out of Let x be the distance of the bottom of the ladder from the wall and let y be the distance of the top of the ladder from the 2 on ground. t' Flag qU95lin What is x in the current problem? Answer: Tlme left 0:59:12 r 4 Ques Ion A 5 ft ladder is placed against a wall. Suppose the bottom of the ladder is sliding away from the wall at a constant rate of 2 feet Silred per second. How fast is the top of the ladder sliding down the wall when the bottom is 3 feet away from the wall? Marked out of Let x be the distance of the bottom of the ladder from the wall and let y be the distance of the top of the ladder from the 2.00 ground. t' Flag QUBSHOF' What is y in the current problem? Hint: Use Pythagorean theorem Answer: Previous Dace L - . - -. - 'l'lme left 0:59:02 r 5 Ques Ion A 5 ft ladder is placed against a wall. Suppose the bottom of the ladder is sliding away from the wall at a constant rate of 2 feet ::;x::ed per second. How fast is the top of the ladder sliding down the wall when the bottom is 3 feet away from the wall? Marked out of Let x be the distance of the bottom of the ladder from the wall and let y be the distance of the top of the ladder from the 2 00 ground. if Flag question What is E . i.e. the rate that x is changing in relation to time. (it Answer: l Previous page Next page Question 6 Not yet answered Marked out of 4.00 F Flag question a moving average-5....mp4 Tlme left 0:58:51 A 5 ft ladder is placed against a wall. Suppose the bottom of the ladder is sliding away from the wall at a constant rate of 2 feet per second. How fast is the top of the ladder sliding down the wall when the bottom is 3 feet away from the wall? Let x be the distance of the bottom of the ladder from the wall and let y be the distance of the top of the ladder from the ground. What is (57:? Le. the rate that y is changing in relation to time. This is where the work will happen. Set up an equation that includes all lengths (use a triangle theorem), differentiate implicitly, and then substitute in values that you know (from the last few questions). Answer: A a candle stick on 2....mp4 A Time left 0:58:43 Question 7 For the interval (a, b), Not yet answered if f (x) > 0 Choose... Marked out of 3.00 if f (x) 0 and f'(x)






























