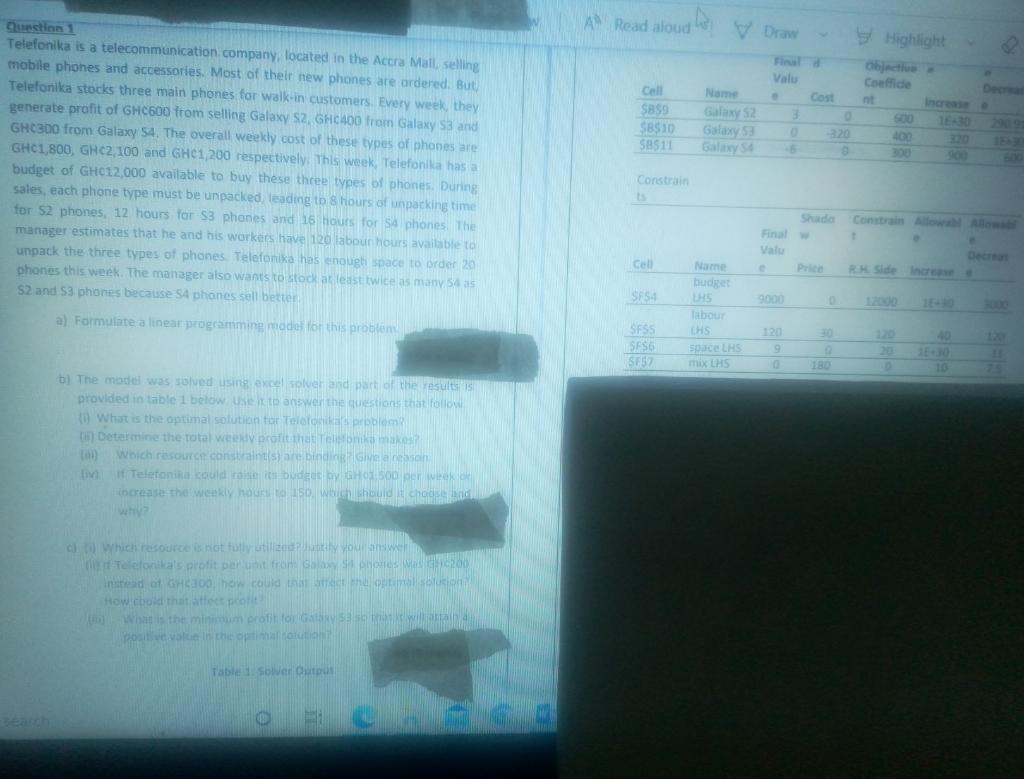
Decreas Cell Sa$9 SB510 SB$11 Name Galaxy S2 Galaxy 53 Galaxy S4 Final de Volu Cost 3 0 320 6 0 Objective Coefficie Increase 500 1430 400 320 300 900 290 90 15.30 500 Question Telefonia is a telecommunication company located in the Accm Mall, selling mobile phones and accessories. Most of their hew phones are ordered. But Telefonika stocks three main phones for walk in customers. Every week, they generate profie SH6600 Wrem selling Galaxy S2 GHCAD from Galaxy 53 and GH4900 from Galiby SA Overall eekly cost of these types of phones are GHCH 800A GHC 100 and GHCL 200 ectively. This week Telefonika has a budget che12 000 ilable these three types of phones. During sales leaca phonesty leading to 8 hours of unpacking time ter 52 phones, di 16 hours for S4 phones. The manager estates the his Workers have o abdul hours available to unpackithe three facial has enough space to order 20 hones this week ger also wants to stock least twice as many as 52 and 53 phones Honeel betret Constrain ts Shado w Final Valu Constrain Allowable Allowa e Decreas RH. Side Increase Cell Price SF$4 9000 12000 15:30 30070 Name budget LHS labour LHS Space LHS mix LHS Formulate near programmine model for this problem 30 SESS $F$6 SFS 120 9 120 20 0 40 1E30 10 AP[10 marks) 180 bThe model was solved using excel solver and part of the results is provided in table 1 below. Use it to answer the questions that follow What is the optimal solution for Telefonikas problem Determine the total Weekly profit that Telefonia makes? Titi Whic Which resource constraints) are bindings Give a reason Teletanika bould raise its budget by GHG 500 per week or Increase the weekly hours to 150, which should it choose and Why ANS marks Whichtesource is not fully utilitedi ustify your answer Telefonika's profil per unit from Galaxy S4 phones wa GHC200 restead of GH800 how could that attect the optimal solution? How could that are prin What is the minimum profit for Galaxy So that it willantaina positive value the optimal solution ANS marks) A Read aloud V Draw Highlight Objectiu Coeffide Valu Cost Cell SBS $B$10 58511 Nam Galaxy Galaxy Galay 3 500 320 Question 1 Telefonika is a telecommunication company, located in the Accra Mall, selling mobile phones and accessories. Most of their new phones are ordered. But) Telefonika stocks three main phones for walk-in customers. Every week, they generate profit of GHC600 from selling Galaxy S2 GHC 400 from Galaxy S3 and GHC300 from Galaxy S4. The overall weekly cost of these types of phones are GHC1,800, GHC2,100 and GHC1,200 respectively. This week, Telefonika hasia budget of GHC12,000 available to buy these three types of phones. During sales, each phone type must be unpacked, leading to 8 hours of unpacking time for 52 phones, 12 hours for S3 phones and 16 hours for $4 phones. The manager estimates that he and his workers have 120 labour hours available to unpack the three types of phones Telefonika has enough space to order 2011 phones this week. The manager also wants to stock at least twice as many 54 as S2 and 53 phones because SA phones sell better a) Formulate a linear programming made for this problem Constrain Shada Final Valu Cell Price SFS 9000 Name budget HS Tabour CHS space LHS mix LHS 120 SFS SFS6 SF5 20 b) The model was solved using excel solve and part of the results provided in table I below Use to answer the questions that follow 10 What is the optimal solution for Telefonike problem h) Determine the total weed profit the lion make Which resource constraints are binding van Telefonia could raisi budet GHS per week Increase the weekly hour to 150, which should chod why c) which resource is not fully utilize on Telefonia's profit per unit from this phones who instead of a how could into How chold that attore profits What is the minimum profit for a show positive in the option Table 1 Sower Output Decreas Cell Sa$9 SB510 SB$11 Name Galaxy S2 Galaxy 53 Galaxy S4 Final de Volu Cost 3 0 320 6 0 Objective Coefficie Increase 500 1430 400 320 300 900 290 90 15.30 500 Question Telefonia is a telecommunication company located in the Accm Mall, selling mobile phones and accessories. Most of their hew phones are ordered. But Telefonika stocks three main phones for walk in customers. Every week, they generate profie SH6600 Wrem selling Galaxy S2 GHCAD from Galaxy 53 and GH4900 from Galiby SA Overall eekly cost of these types of phones are GHCH 800A GHC 100 and GHCL 200 ectively. This week Telefonika has a budget che12 000 ilable these three types of phones. During sales leaca phonesty leading to 8 hours of unpacking time ter 52 phones, di 16 hours for S4 phones. The manager estates the his Workers have o abdul hours available to unpackithe three facial has enough space to order 20 hones this week ger also wants to stock least twice as many as 52 and 53 phones Honeel betret Constrain ts Shado w Final Valu Constrain Allowable Allowa e Decreas RH. Side Increase Cell Price SF$4 9000 12000 15:30 30070 Name budget LHS labour LHS Space LHS mix LHS Formulate near programmine model for this problem 30 SESS $F$6 SFS 120 9 120 20 0 40 1E30 10 AP[10 marks) 180 bThe model was solved using excel solver and part of the results is provided in table 1 below. Use it to answer the questions that follow What is the optimal solution for Telefonikas problem Determine the total Weekly profit that Telefonia makes? Titi Whic Which resource constraints) are bindings Give a reason Teletanika bould raise its budget by GHG 500 per week or Increase the weekly hours to 150, which should it choose and Why ANS marks Whichtesource is not fully utilitedi ustify your answer Telefonika's profil per unit from Galaxy S4 phones wa GHC200 restead of GH800 how could that attect the optimal solution? How could that are prin What is the minimum profit for Galaxy So that it willantaina positive value the optimal solution ANS marks) A Read aloud V Draw Highlight Objectiu Coeffide Valu Cost Cell SBS $B$10 58511 Nam Galaxy Galaxy Galay 3 500 320 Question 1 Telefonika is a telecommunication company, located in the Accra Mall, selling mobile phones and accessories. Most of their new phones are ordered. But) Telefonika stocks three main phones for walk-in customers. Every week, they generate profit of GHC600 from selling Galaxy S2 GHC 400 from Galaxy S3 and GHC300 from Galaxy S4. The overall weekly cost of these types of phones are GHC1,800, GHC2,100 and GHC1,200 respectively. This week, Telefonika hasia budget of GHC12,000 available to buy these three types of phones. During sales, each phone type must be unpacked, leading to 8 hours of unpacking time for 52 phones, 12 hours for S3 phones and 16 hours for $4 phones. The manager estimates that he and his workers have 120 labour hours available to unpack the three types of phones Telefonika has enough space to order 2011 phones this week. The manager also wants to stock at least twice as many 54 as S2 and 53 phones because SA phones sell better a) Formulate a linear programming made for this problem Constrain Shada Final Valu Cell Price SFS 9000 Name budget HS Tabour CHS space LHS mix LHS 120 SFS SFS6 SF5 20 b) The model was solved using excel solve and part of the results provided in table I below Use to answer the questions that follow 10 What is the optimal solution for Telefonike problem h) Determine the total weed profit the lion make Which resource constraints are binding van Telefonia could raisi budet GHS per week Increase the weekly hour to 150, which should chod why c) which resource is not fully utilize on Telefonia's profit per unit from this phones who instead of a how could into How chold that attore profits What is the minimum profit for a show positive in the option Table 1 Sower Output