Derive Eq. (1) using the optical path diagram shown in Fig. 1. Briefly describe the physical meaning of Eq. (1).

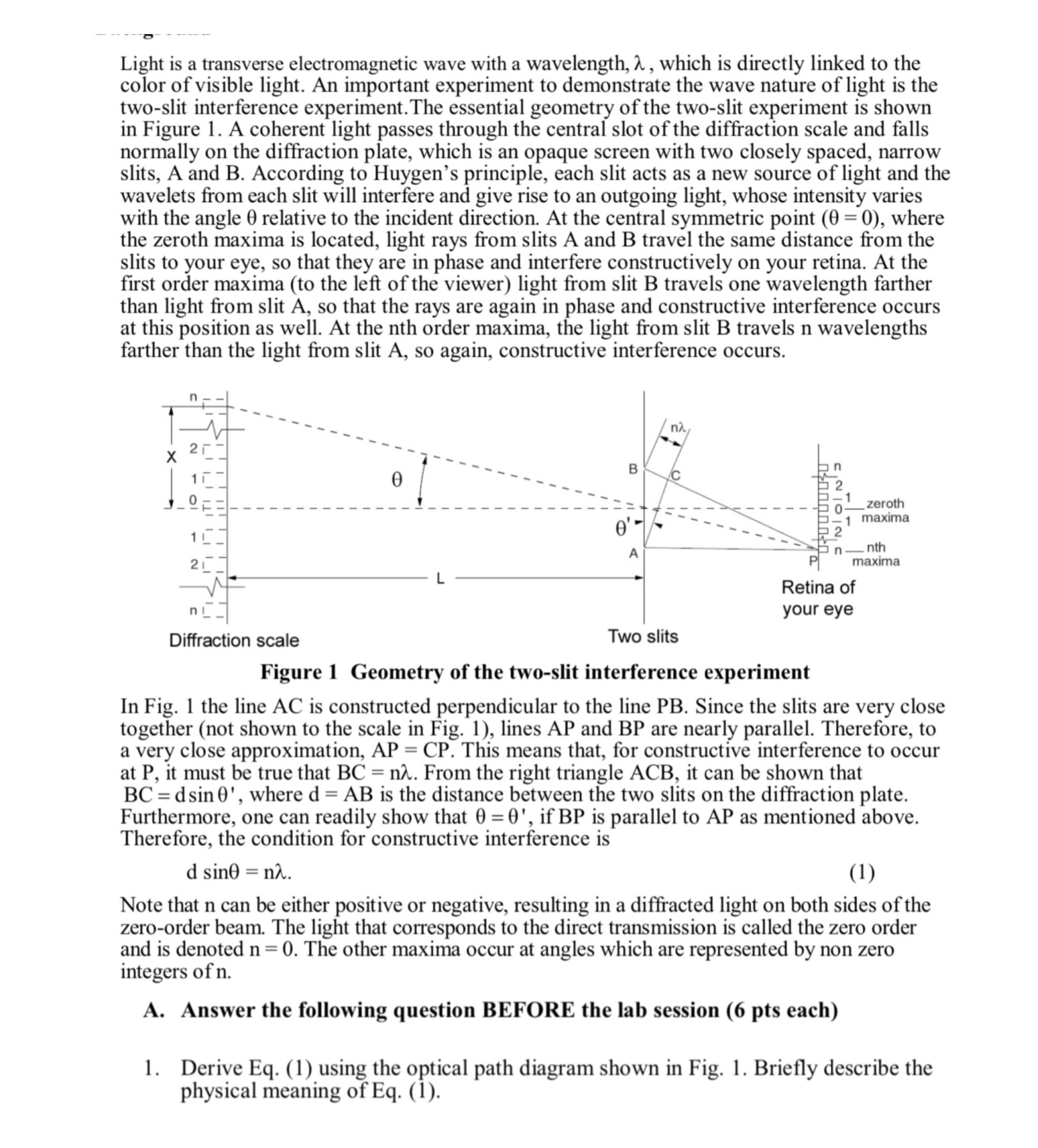
Light is a transverse electromagnetic wave with a wavelength, A , which is directly linked to the color of visible light. An important experiment to demonstrate the wave nature of light is the two-slit interference experiment.The essential geometry of the two-slit experiment is shown in Figure l. A coherent light passes through the central slot of the diffraction scale and falls normally on the diffraction plate, which is an opaque screen with two closely spaced, narrow slits, A and B. According to Huygen's principle, each slit acts as a new source of light and the wavelets from each slit will interfere and give rise to an outgoing light, whose intensity varies with the angle 9 relative to the incident direction. At the central symmetric point (9 = 0), where the zeroth maxima is located, light rays -om slits A and B travel the same distance 'om the slits to your eye, so that they are in phase and interfere constructively on your retina. At the rst order maxima (to the left of the viewer) light from slit B travels one wavelength farther than light from slit A, so that the rays are again in phase and constructive interference occurs at this position as well. At the nth order maxima, the light 'om slit B travels n wavelengths farther than the light 'om slit A, so again, constructive interference occurs. your eye Two slits Figure 1 Geometry of the two-slit interference experiment In Fig. l the line AC is constructed perpendicular to the line PB. Since the slits are very close together (not shown to the scale in Fig. 1), lines AP and BP are nearly parallel. Therefore, to a very close approximation, AP = CP. This means that, for constructive interference to occur at P, it must be true that BC = 11A. From the right triangle ACB, it can be shown that BC = dsine' , where d = AB is the distance between the two slits on the di'raction plate. Furthermore, one can readily show that 0 = 9', if BP is parallel to AP as mentioned above. Therefore, the condition for constructive interference is dsinB=n2L (1) Note that n can be either positive or negative, resulting in a diffracted light on both sides of the zero-order beam. The light that corresponds to the direct transmission is called the zero order and is denoted n = 0. The other maxima occur at angles which are represented by non zero integers of n. A. Answer the following question BEFORE the lab session (6 pts each) 1. Derive Eq. (1) using the optical path diagram shown in Fig. 1. Briey describe the physical meaning of Eq. (I)