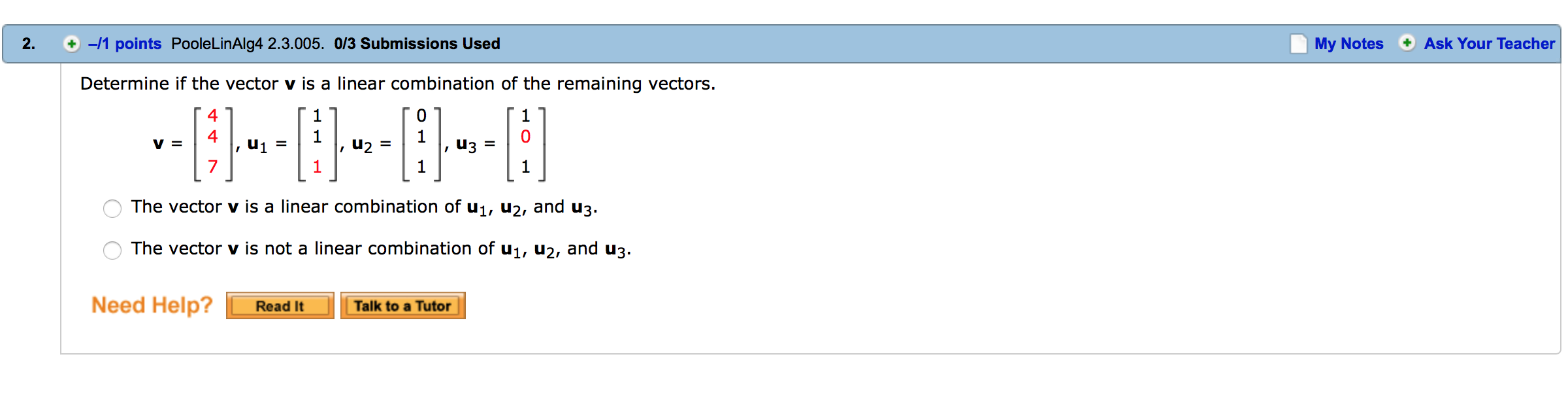
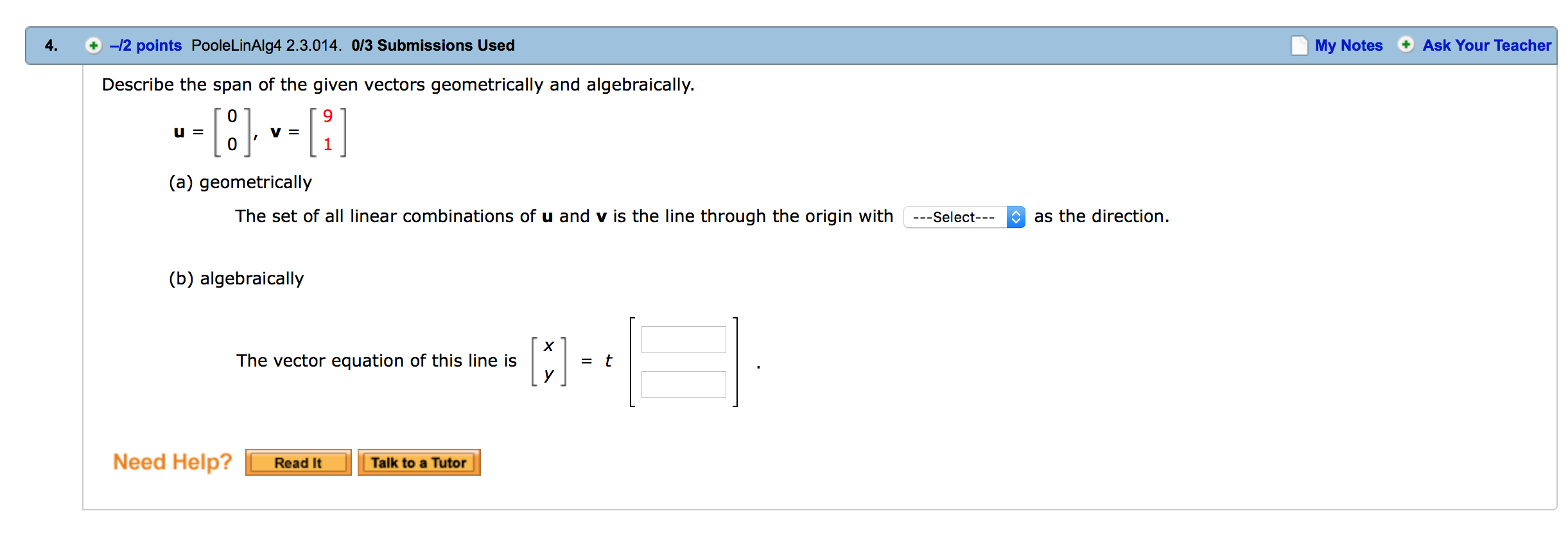
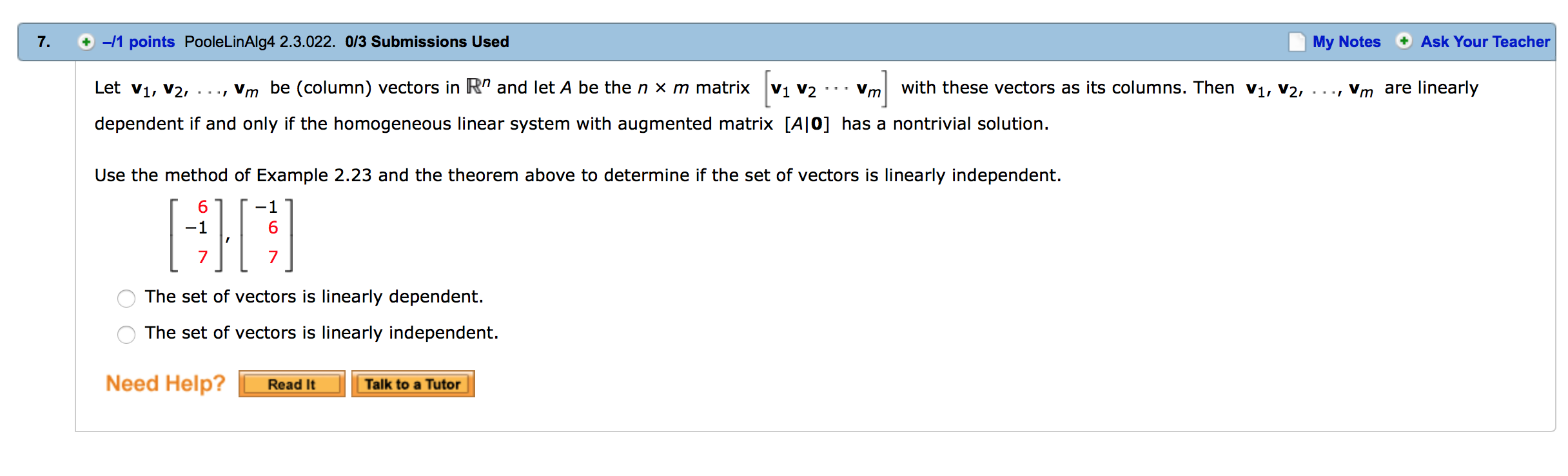
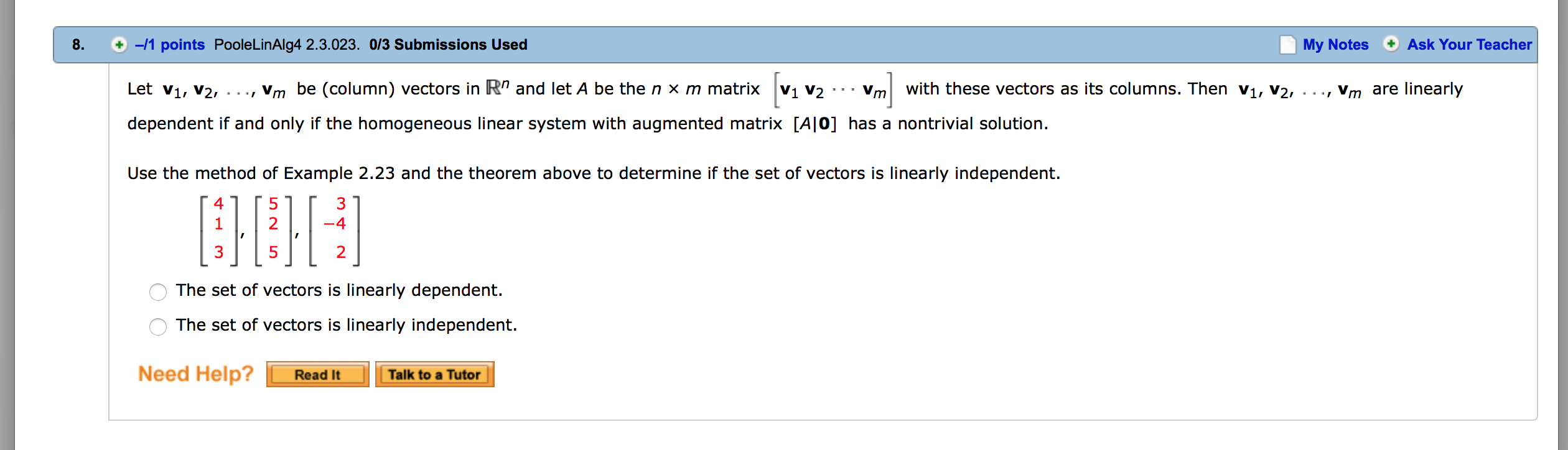
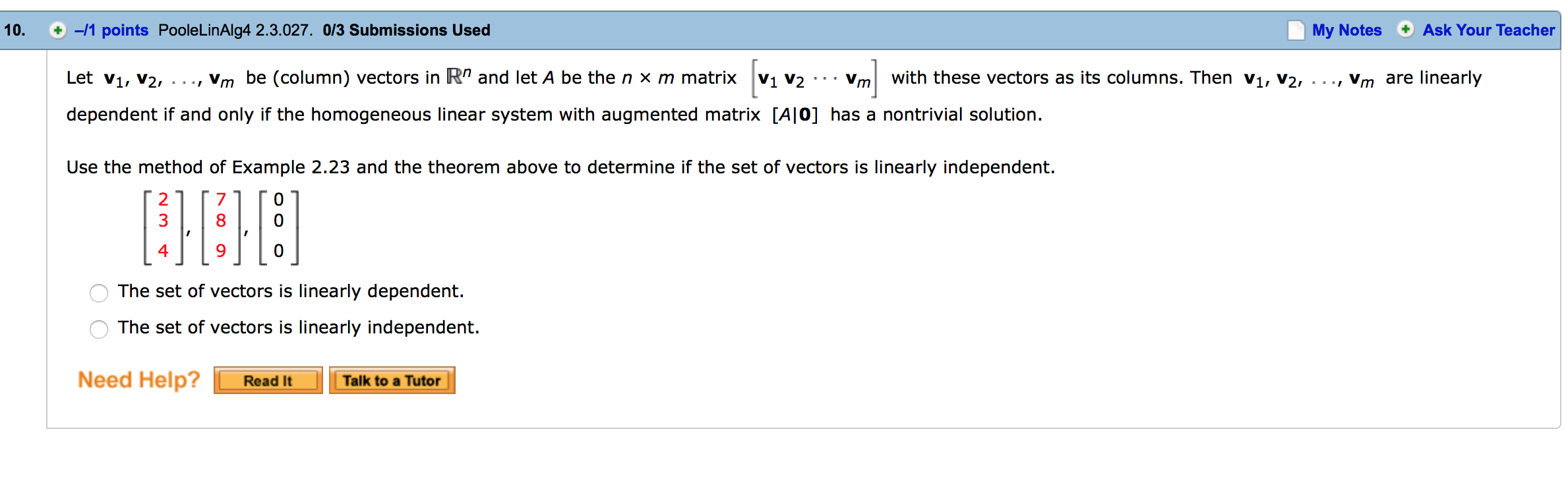
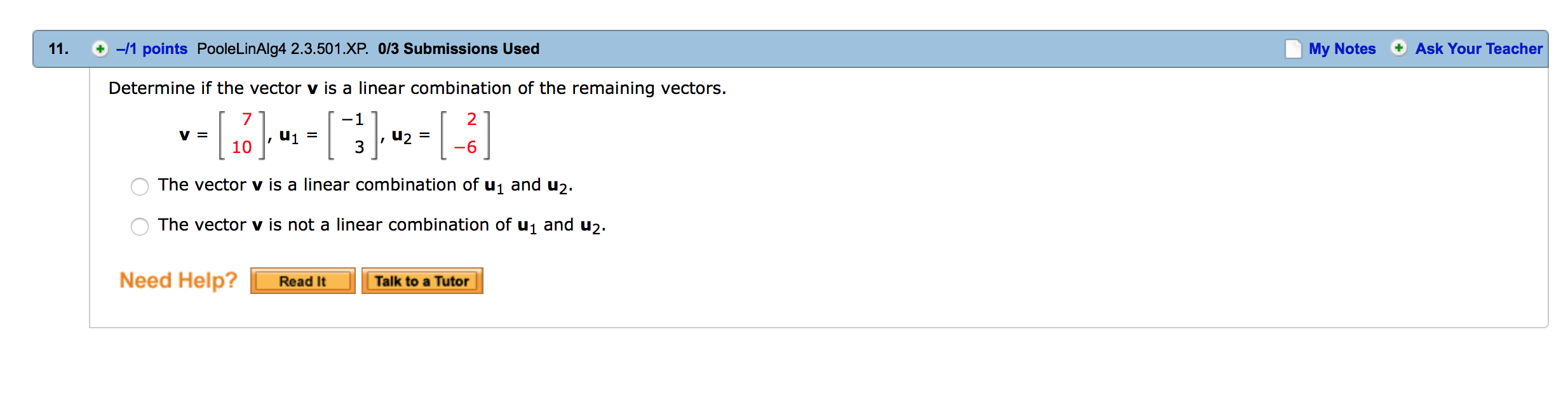
Determine if the vector v is a linear combination of the remaining vectors. v=[:1~1=[-:1~2=[:J O The vector v is a linear combination of ul and uz. O The vector v is not a linear combination of u1 and uz. Need Help? i i Determine if the vector v is a linear combination of the remaining vectors. 4 1 o 1 V= 4.U1= 1,02= 1,u3= 7 1 1 1 Q The vector v is a linear combination of u1, uz, and u3. O The vector v is not a linear combination of u1, uz, and u3. Need Help? ii 1 1 2 Show that R3 =span 1 , 2 , 1 . 0 3 1 We want to show that any vector can be written as a linear combination of the three given vectors, i.e. that [EHitH'iE] for some x, y, z. Row-reduce the associated augmented matrix: 112 112 11 2 a R2-R1 REX3R2 1211) 011 011 03-1 C 03-1 002 112 110 R1-2R3 iR ' 23011 010 D R2+R3 ) 001 001 100 R1_R2 010 001 Describe the span of the given vectors geometrically and algebraically. \"mum (a) geometrically The set of all linear combinations of u and v is the line through the origin with -Se|ect-- as the direction. (b) algebraically x The vector equation of this line is [ y] = t Need Help? i i Describe the span of the given vectors geometrically and algebraically. "=lil~=lfl (a) geometrically O The set of all linear combinations of u and v is a plane through the origin containing u and v as direction vectors. 0 The set of all linear combinations of u and v is the line through the origin with v as the direction. Q The set of all linear combinations of u and v is a plane through the origin containing only u as a direction vector. 0 The set of all linear combinations of u and v is the line through the origin with u as the direction. 0 The set of all linear combinations of u and v is a plane through the origin containing only v as a direction vector. (b) algebraically x 1 The vector equation of this plane is [y] = s[ 5:| + t z 0 Need Help? i i The general equation of the plane that contains the points (1, 0, 8), (1, 1, 8), and the origin is of the form ax + by + a = 0. Solve for a, b, and c. (Enter the equation of the plane.) : Need new ii Let v1, v2, . . ., vm be (column) vectors in R\" and letA be the n X m matrix [v1 v2 - - - vm] with these vectors as its columns. Then v1, v2, . . ., v\Let v1, v2, . .., vm be (column) vectors in R" and let A be the n x m matrix [v1 v2 -- - vm] with these vectors as its columns. Then v1, v2, . . ., V," are linearly dependent if and only if the homogeneous linear system with augmented matrix [A|O] has a nontrivial solution. Use the method of Example 2.23 and the theorem above to determine if the set of vectors is linearly independent. [ZHEH'E Q The set of vectors is linearly dependent. O The set of vectors is linearly independent. Need Help? ii Let v1, v2, . .., V\Let v1, v2, . . ., V,\" be (column) vectors in R\" and letA be the n x m matrix [v1 v2 -- - vm] with these vectors as its columns. Then v1, v2, . .., vm are linearly dependent if and only if the homogeneous linear system with augmented matrix [AIO] has a nontrivial solution. Use the method of Example 2.23 and the theorem above to determine if the set of vectors is linearly independent. 2 7 0 3 8 0 I l 4 9 0 O The set of vectors is linearly dependent. Q The set of vectors is linearly independent. Need Help? _ #s Determine if the vector v is a linear combination of the remaining vectors. v=[1;].u1=[-:J~z=[_:1 Q The vector v is a linear combination of u1 and uz. O The vector v is not a linear combination of 1:1 and uz. Need Help? i i \f