 Determine the confidence interval for beta1, predicted value, average value, prediction interval, given xp
Determine the confidence interval for beta1, predicted value, average value, prediction interval, given xp





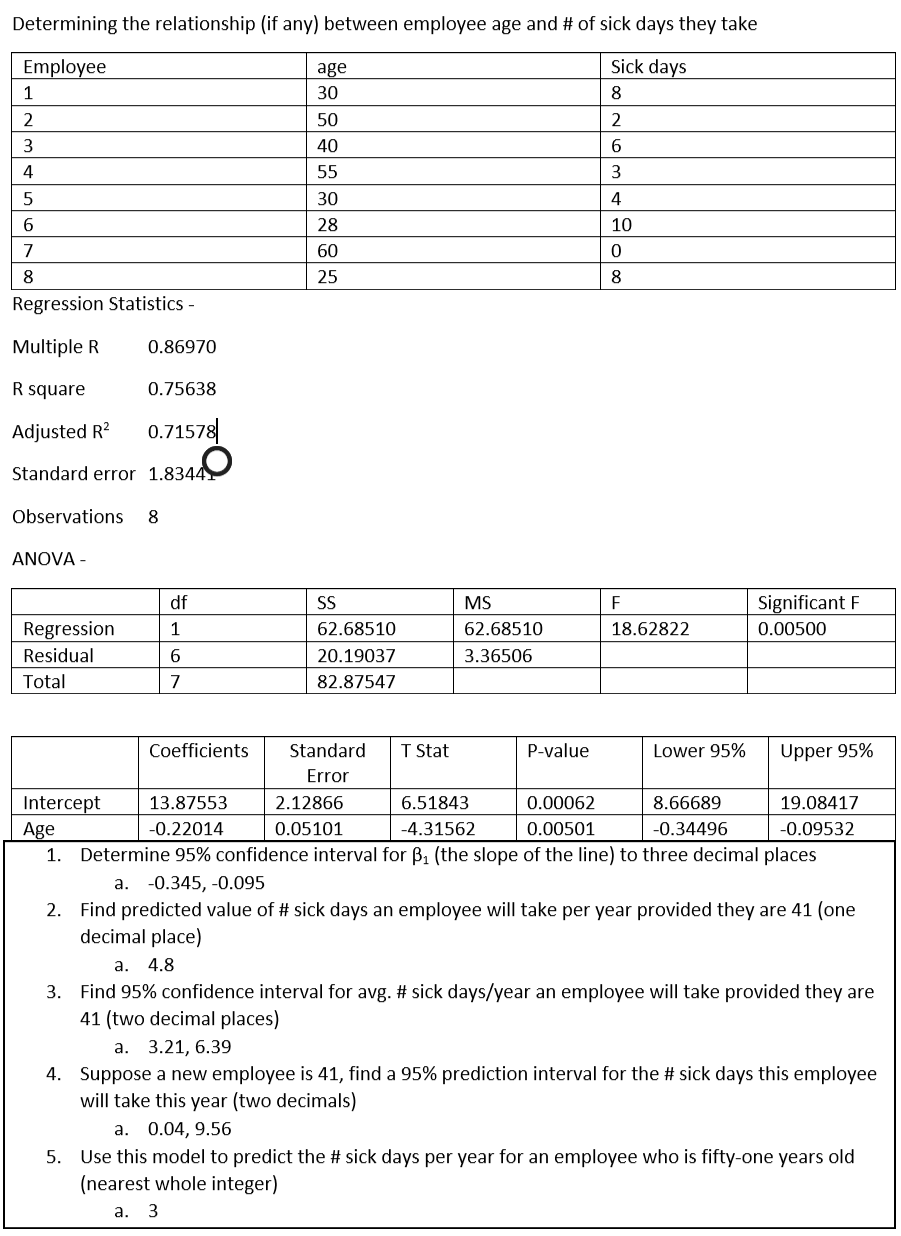
Determining the relationship (if any) between employee age and # of sick days they take Employee age Sick days 30 50 40 6 | 3 55 30 | 7 600 258 Regression Statistics - Multiple R 0.86970 R square 0.75638 Adjusted R2 0.71578 Standard error 1.8344 Observations 8 ANOVA - df F Significant F 0.00500 M S 62.68510 3.36506 Regression Residual Total 18.62822 SS 62.68510 20.19037 82.87547 Coefficients Standard T Stat P-value Lower 95% Upper 95% Error Intercept 13.87553 2 .12866 6.51843 0.00062 8.66689 19.08417 Age -0.22014 0.05101 -4.31562 0.00501 -0.34496 -0.09532 1. Determine 95% confidence interval for B1 (the slope of the line) to three decimal places a. -0.345,-0.095 2. Find predicted value of #sick days an employee will take per year provided they are 41 (one decimal place) a. 4.8 3. Find 95% confidence interval for avg. #sick days/year an employee will take provided they are 41 (two decimal places) a. 3.21, 6.39 4. Suppose a new employee is 41, find a 95% prediction interval for the #sick days this employee will take this year (two decimals) a. 0.04, 9.56 5. Use this model to predict the #sick days per year for an employee who is fifty-one years old (nearest whole integer) a. 3 Simple Linear Regression Model y, = Be + B,x,+; Estimated Simple Linear Regression Equation , = be +b, x; Sum of Squared Errors SSE = E(y 5) = {(y;-(bo+b,x;))? Slope of the Least Squares Line y-Intercept of the Least Squares Line bo = 5 6,5=(. v, -6, x) Mean Square Error 222 =)_sse SSE n-2 n -2 Standard Error 2(y-) SSE n- 2 Vn-2 Total Sum of Squares TSS = E(y; -7) TSS=SSE + SSR Sum of Squares of Regression SSR = TSS-SSE Coefficient of Determination SSR R? - SSR, SSE SSE TSS TSS Sample Estimate of the Variance of b, Sample Estimate of the Standard Deviation (Standard Error) of b, VE(x; -7) 100(1 - a)% Confidence Interval for B bi Ft./2.01 Son Test Statistic for Testing the Hypothesis B, 70 1 = 60 by 100(1-a)% Confidence Interval for the Mean Value of y, given x = Xp: y Eta/25, pevn (x,-F) 100(1-a)% Prediction Interval for the Value of y, given x = Xp: 11 (x,-.7) y Eta/29,1+-+ aze y n. (.x; 7) Multiple Regression Model y; = B. +3,x; + Bxz; +...+ BXxi +8, Estimated Multiple Regression Equation y = b + bx + b,x, ++bx Adjusted RP (n-1 SSE R2 =1-1- (n-k-1) TSS F-Statistic Sum of Squares of Regression F=- Sum of Squared Errors n-(k+1) SSR k Mean Square Regression SSE Mean Square Error n-(k+1) 100(1 - a)% Confidence Interval for Individual Coefficients b; +12/2.df Sb Test Statistic for Testing the Hypothesis 3,60 7 = b;-0 _b Determining the relationship (if any) between employee age and # of sick days they take Employee age Sick days 30 50 40 6 | 3 55 30 | 7 600 258 Regression Statistics - Multiple R 0.86970 R square 0.75638 Adjusted R2 0.71578 Standard error 1.8344 Observations 8 ANOVA - df F Significant F 0.00500 M S 62.68510 3.36506 Regression Residual Total 18.62822 SS 62.68510 20.19037 82.87547 Coefficients Standard T Stat P-value Lower 95% Upper 95% Error Intercept 13.87553 2 .12866 6.51843 0.00062 8.66689 19.08417 Age -0.22014 0.05101 -4.31562 0.00501 -0.34496 -0.09532 1. Determine 95% confidence interval for B1 (the slope of the line) to three decimal places a. -0.345,-0.095 2. Find predicted value of #sick days an employee will take per year provided they are 41 (one decimal place) a. 4.8 3. Find 95% confidence interval for avg. #sick days/year an employee will take provided they are 41 (two decimal places) a. 3.21, 6.39 4. Suppose a new employee is 41, find a 95% prediction interval for the #sick days this employee will take this year (two decimals) a. 0.04, 9.56 5. Use this model to predict the #sick days per year for an employee who is fifty-one years old (nearest whole integer) a. 3 Simple Linear Regression Model y, = Be + B,x,+; Estimated Simple Linear Regression Equation , = be +b, x; Sum of Squared Errors SSE = E(y 5) = {(y;-(bo+b,x;))? Slope of the Least Squares Line y-Intercept of the Least Squares Line bo = 5 6,5=(. v, -6, x) Mean Square Error 222 =)_sse SSE n-2 n -2 Standard Error 2(y-) SSE n- 2 Vn-2 Total Sum of Squares TSS = E(y; -7) TSS=SSE + SSR Sum of Squares of Regression SSR = TSS-SSE Coefficient of Determination SSR R? - SSR, SSE SSE TSS TSS Sample Estimate of the Variance of b, Sample Estimate of the Standard Deviation (Standard Error) of b, VE(x; -7) 100(1 - a)% Confidence Interval for B bi Ft./2.01 Son Test Statistic for Testing the Hypothesis B, 70 1 = 60 by 100(1-a)% Confidence Interval for the Mean Value of y, given x = Xp: y Eta/25, pevn (x,-F) 100(1-a)% Prediction Interval for the Value of y, given x = Xp: 11 (x,-.7) y Eta/29,1+-+ aze y n. (.x; 7) Multiple Regression Model y; = B. +3,x; + Bxz; +...+ BXxi +8, Estimated Multiple Regression Equation y = b + bx + b,x, ++bx Adjusted RP (n-1 SSE R2 =1-1- (n-k-1) TSS F-Statistic Sum of Squares of Regression F=- Sum of Squared Errors n-(k+1) SSR k Mean Square Regression SSE Mean Square Error n-(k+1) 100(1 - a)% Confidence Interval for Individual Coefficients b; +12/2.df Sb Test Statistic for Testing the Hypothesis 3,60 7 = b;-0 _b
 Determine the confidence interval for beta1, predicted value, average value, prediction interval, given xp
Determine the confidence interval for beta1, predicted value, average value, prediction interval, given xp 










