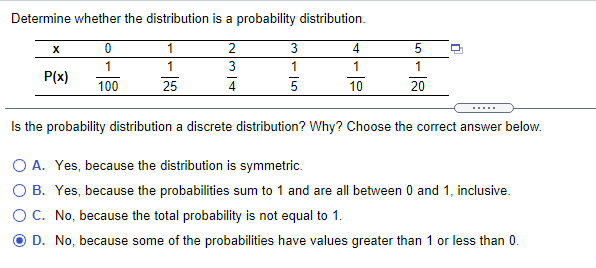

Determine whether the distribution is a probability distribution. It 11 1 2 3 :1 5 Q1 1 3 1 1 1 p _ _ _ _ _ _ III 1111] 25 4 5 111 211 Is the probability distribution a discrete distribution? Why? Choose the conect answer below. CI r. Yes, because the distribution is symmetric. CI E. Yes, because the probabilities sum to 1 and are all between If] and 1, inclusive. Cl C. No, because the total probability is not equal to 1. {El D. No, because some of the probabilities have 1tI'alues greater than 1 or less than El. In a recent veer, the mean number of strokes per hole for a famous golfer was approximatelv 3.2. {a} Find the variance and standard deviation using the fact that the variance of a Poisson distribution is o2 = p. {b} How likely:r is this golfer to playr an 18-hole round and have more than T2 strokes? .m- [a} The variance is -. {Round to the nearest tenth as needed.) The standard deviation is strokes. [Round to the nearest tenth as needed.) {b} The probability of more than 7'2 strokes in an 13hole round is ELEIEE . [Round to the nearest thousandth as needed} Use the probability distribution to complete parts (a) and (b) below. The number ot defects per 1000 machine parts inspected Defects U 1 2 3 4 5 g. Probability 0.250 0.293 0.241 0.139 [1.045 [1.017 .m- (3) Find the mean, variance, and standard deviation of the probability distribution. The mean is -. (Round to one decimal place as needed.) The variance is 0.01 . (Round to one decimal place as needed.) The standard deviation is -. (Round to one decimal place as needed.) (b) Interpret the results. The mean is I, so the average batch of 1000 machine parts has 1 or 2 defects. The standard deviation is -, so the typical number of defects in a batch of 1000 deviates from the mean by more than 2 defects. (Round to one decimal place as needed.) 1 Use the fact that the mean of a geometric distribution is p: and the variance is 02 = 2 . P p 1 Adaily number lottery chooses two balls numbered 0 to 9. The probability of winning the lottery is W' Let): be the number of times you play the lottery before winning the rst time. (a) Find the mean, variance, and standard deviation. (b) How many times would you expect to have to play the lottery before winning? It costs $1 to play and winners are paid $300. Would you expect to make or lose money playing this lottery? Explain. (a) The mean is El. (Type an integer or a decimal.) The variance is :|. [Type an integer or a decimal} The standard deviation is El. (Round to one decimal place as needed.) (b) You can expect to play the game I: times before winning. Would you expect to make or lose money playing this lottery? Explain. O A- You would expect to make money. On average you would win $800 once in every I: times you play. So the net gain would be $|:. O B- You would expect to lose money. On average you would win $300 once in every D times you play. So the net gain would be $|:| Two random variables x and y are independent if the value of): does not affect the value of v. If the variables are not independent, they are dependent Anew random variable can be formed by nding the sum or difference of random van'ables. lfa random variable x has mean l1): and a random variable y has mean u), then the means of the sum and difference of the van'ables are given by the following equations. "x+v:\"3