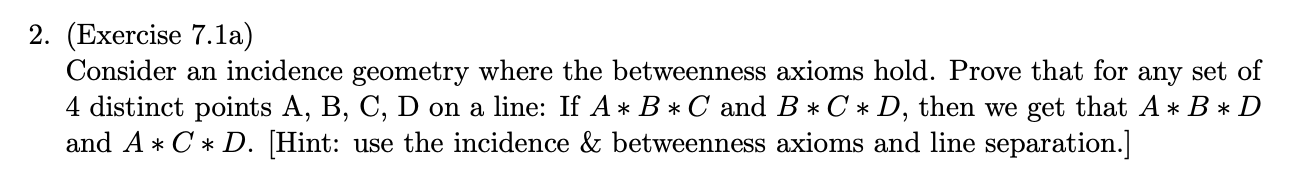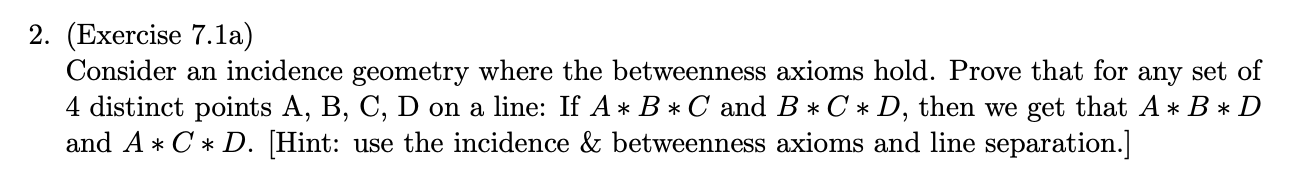
DIRECTIONS: For each of the following questions, you may only site propositions 6.1, 7.1, 7.2, and 7.3; the incidence axioms, the betweenness axioms, and any definition from sections 6 & 7 of Hartshorne's textbook. You may also use exercises from the textbook, but only if you (or we as a class) have proved them and their number comes before whatever exercise you are trying to use it to prove. 2. (Exercise 7.1a) Consider an incidence geometry where the betweenness axioms hold. Prove that for any set of 4 distinct points A, B, C, D on a line: If A * B * C and B * C * D, then we get that A * B * D and A* C * D. (Hint: use the incidence & betweenness axioms and line separation.] Proposition 7.1 (Plane separation) Let l be any line. Then the set of points not lying on l can be divided into two non- empty subsets S1, S2 with the following properties: (a) Two points A, B not on 1 belong to the same set (Si or S2) if and only if the segment AB does not intersect 1. (b) Two points A, C not on l belong to the opposite sets (one in S, the other in S2) if and only if the segment AC in- l l tersects l in a point. We will refer to the sets S1, S2 as the two sides of l, and we will say "A and B are on the same side of l," or "A and C are on opposite sides of l." C 7. Axioms of Betweenness 75 Proof We start by defining a relation ~ among points not on 1. We will say A ~ B if either A = B or if the segment AB does not meet l. Our first step is to show that is an equivalence relation. Clearly, A ~ A by definition, and A ~ B implies B ~ A because the set AB does not depend on the order in which we write A and B. The nontrivial step is to show the relation is transitive: If A B and B ~ C, we must show A ~ C. A Case 1 Suppose A,B,C are not col- linear. Then we consider the triangle ABC. Since A ~B, I does not meet AB. Since B - C, 1 does not meet BC. Now by Pasch's axiom (B4), it follows that I does not meet AC. Hence A - C. e LE C A e Case 2 Suppose A,B,C lie on a line m. Since A, B, C do not lie on l, the line m is different from I. Therefore I and m can meet in at most one point (6.1). But by (12) every line has at least two points. Therefore, there exists a point D on 1, D not lying on m. Now apply axiom (B2) to find a point E such that D* A * E. Then D, A, E are collinear (B1); hence E is not on l, since A is not on l, and the line DAE already meets I at the point D. Furthermore, the segment AE cannot meet l. For if it did, the intersection point would be the unique point in which the line AE meets 1, namely D. In that case D would be between A and E. But we con- structed E so that D* A * E, so by (B3), D cannot lie between A and E. Thus AENT= 0, so A E. Note also that E does not lie on the line m, because if E were on m, then the line AE would be equal to m, so D would lie on m, contrary to our choice of D. Therefore, A,B, E are three noncollinear points. Then by Case 1 proved above, from A ~ E and A ~ B we conclude B ~ E. By Case 1 again, from B~ E and B ~ C we conclude C ~ E. Applying Case 1 a third time to the three noncollinear points A, C, E, from A ~ E and C ~ E we conclude A C as required. Thus we have proved that ~ is an equivalence relation. An equivalence relation on a set divides that set into a disjoint union of equivalence classes, and these equivalence classes will satisfy property (a) by definition. To complete the proof it will be sufficient to show that there are exactly two equivalence classes S1, S2 for the relation ~. Then to say that AC meets I, which is equivalent to A + C, will be the same as saying that A, C belong to the opposite sets. By (13) there exists a point not onl, so there is at least one equivalence class Sj. Given A S1, let D be any point on l, and choose by (B2) a point C such that A *D* C. Then A and C do not satisfy ~ so there must be at least two equiva- lence classes S and S2. The last step is to show that there are at most two equivalence classes. To do this, we will show that if A * C and B * C, then A B. A B Case 1 If A, B, C are not collinear, we consider the triangle ABC. From A C we conclude that AC meets 1. From B* we conclude that BC meets 1. Now by Pasch's axiom (B4) it follows that AB does not meet 1. So A - B as required. V A D Case 2 Suppose A, B, C lie on a line m. As in Case 2 of the first part of the proof above, choose a point D on l, not on m, and use (B2) to get a point E with D* A * E. Then A - E as we showed above. Now, A * C by hypothesis, and A ~ E, so we conclude that C + E, since is an equivalence relation (if C ~ E, then A ~ by transitivity: contradiction). Looking at the three noncollinear points B, C, E, from E + C and B+C we conclude using Case 1 that B ~ E. But also A ~ E, so by transitivity, A ~ B as required. Proposition 7.2 (Line separation) Let A be a point on a line l. Then the set of points of l not equal to A can be divided into two nonempty subsets Si, S2, the two sides of A on l, such that (a) B, C are on the same side of A if and only if A is not in the segment BC; D C e (b) B, D are on opposite sides of A if and only if A belongs to the segment BD 'm E Proof Given the line l and a point A on 1, we know from (13) that there exists a point E not on l. Let m be the line con- taining A and E. Apply (7.1) to the line m. If m has two sides S, S, we define S and S2 to be the intersections of S and Sy with 1. Then properties (a) and (b) follow immediately from the previous proposition. A I 7. Axioms of Betweenness 77 The only mildly nontrivial part is to show that S and S2 are nonempty. By (12), there is a point B on l different from A. And by (B2) there exists a point D such that B * A * D. Then D will be on the opposite side of A from B, and will lie on l, so both sides are nonempty. Now that we have some basic results on betweenness, we can define rays and angles. A B B Definition Given two distinct points A, B, the ray AB is the set consisting of A, plus all points on the line AB that are on the same side of A as B. The point A is the origin, or vertex, of the ray. An angle is the union of two rays AB and AC originating at the same point, its vertex, and not lying on the same line. (Thus there is no "zero angle," and there is no "straight angle" (180).) Note that the vertex of a ray or angle is uniquely de- termined by the ray or angle (proof similar to Exercises 7.2, 7.3). The inside (or interior) of an angle BAC consists of all points D such that D and C are on the same side of the line AB, and D and B are on the same side of the line AC. If ABC is a triangle, the in- side (or interior) of the triangle ABC is the set of points that are simultaneously in the insides of the three angles LBAC, LABC, LACB. B B D Proposition 7.3 (Crossbar theorem) Let LBAC be an angle, and let D be a point in the interior of the angle. Then the ray AD must meet the segment BC. Proof This is similar to Pasch's axiom (B4), except that we must consider a line AD that passes through one vertex of the triangle ABC. We will prove it with Pasch's axiom and several applications of the plane separation theorem (7.1). D E A c Let us label the lines AB = 1, AC = m, AD = n. Let E be a point on m such 3 that E* A * C(B2). We will apply Pasch's axiom (B4) to the triangle BCE and the line n. By construction n meets the side CE at A. Also, n cannot contain B, be- cause it meets the line 1 at A. We will show that n does not meet the segment BE, so as to conclude by (B4) that it must meet the segment BC. So we consider the segment BE. This segment meets the line l only at B, so all points of the segment, except B, are on the same side of 1. By construction, is on the opposite side of 1 from E, so by (7.1) all points of BE, except B, are on the opposite side of 1 from C. On the other hand, since D is in the interior of the angle _BAC, all the points of the ray AD, except A, are on the same side of l as C. Thus the segment BE does not meet the ray AD. A similar reasoning using the line m shows that all points of the segment BE, except E, lie on the same side of m as B, while the points of the ray of n, opposite the ray AD, lie on the other side of m. Hence the segment BE cannot meet the opposite ray to AD. Together with the previous step, this shows that the seg- ment BE does not meet the line n. We conclude by (B4) that n meets the seg- ment BC in a point F. It remains only to show that F is on the ray AD of the line n. Indeed, B and Fare on the same side of m, and also B and D are on the same side of m, so (7.1) D and F are on the same side of m, and so D and F are on the same side of A on the line n. In other words, F lies on the ray AD. DIRECTIONS: For each of the following questions, you may only site propositions 6.1, 7.1, 7.2, and 7.3; the incidence axioms, the betweenness axioms, and any definition from sections 6 & 7 of Hartshorne's textbook. You may also use exercises from the textbook, but only if you (or we as a class) have proved them and their number comes before whatever exercise you are trying to use it to prove. 2. (Exercise 7.1a) Consider an incidence geometry where the betweenness axioms hold. Prove that for any set of 4 distinct points A, B, C, D on a line: If A * B * C and B * C * D, then we get that A * B * D and A* C * D. (Hint: use the incidence & betweenness axioms and line separation.] Proposition 7.1 (Plane separation) Let l be any line. Then the set of points not lying on l can be divided into two non- empty subsets S1, S2 with the following properties: (a) Two points A, B not on 1 belong to the same set (Si or S2) if and only if the segment AB does not intersect 1. (b) Two points A, C not on l belong to the opposite sets (one in S, the other in S2) if and only if the segment AC in- l l tersects l in a point. We will refer to the sets S1, S2 as the two sides of l, and we will say "A and B are on the same side of l," or "A and C are on opposite sides of l." C 7. Axioms of Betweenness 75 Proof We start by defining a relation ~ among points not on 1. We will say A ~ B if either A = B or if the segment AB does not meet l. Our first step is to show that is an equivalence relation. Clearly, A ~ A by definition, and A ~ B implies B ~ A because the set AB does not depend on the order in which we write A and B. The nontrivial step is to show the relation is transitive: If A B and B ~ C, we must show A ~ C. A Case 1 Suppose A,B,C are not col- linear. Then we consider the triangle ABC. Since A ~B, I does not meet AB. Since B - C, 1 does not meet BC. Now by Pasch's axiom (B4), it follows that I does not meet AC. Hence A - C. e LE C A e Case 2 Suppose A,B,C lie on a line m. Since A, B, C do not lie on l, the line m is different from I. Therefore I and m can meet in at most one point (6.1). But by (12) every line has at least two points. Therefore, there exists a point D on 1, D not lying on m. Now apply axiom (B2) to find a point E such that D* A * E. Then D, A, E are collinear (B1); hence E is not on l, since A is not on l, and the line DAE already meets I at the point D. Furthermore, the segment AE cannot meet l. For if it did, the intersection point would be the unique point in which the line AE meets 1, namely D. In that case D would be between A and E. But we con- structed E so that D* A * E, so by (B3), D cannot lie between A and E. Thus AENT= 0, so A E. Note also that E does not lie on the line m, because if E were on m, then the line AE would be equal to m, so D would lie on m, contrary to our choice of D. Therefore, A,B, E are three noncollinear points. Then by Case 1 proved above, from A ~ E and A ~ B we conclude B ~ E. By Case 1 again, from B~ E and B ~ C we conclude C ~ E. Applying Case 1 a third time to the three noncollinear points A, C, E, from A ~ E and C ~ E we conclude A C as required. Thus we have proved that ~ is an equivalence relation. An equivalence relation on a set divides that set into a disjoint union of equivalence classes, and these equivalence classes will satisfy property (a) by definition. To complete the proof it will be sufficient to show that there are exactly two equivalence classes S1, S2 for the relation ~. Then to say that AC meets I, which is equivalent to A + C, will be the same as saying that A, C belong to the opposite sets. By (13) there exists a point not onl, so there is at least one equivalence class Sj. Given A S1, let D be any point on l, and choose by (B2) a point C such that A *D* C. Then A and C do not satisfy ~ so there must be at least two equiva- lence classes S and S2. The last step is to show that there are at most two equivalence classes. To do this, we will show that if A * C and B * C, then A B. A B Case 1 If A, B, C are not collinear, we consider the triangle ABC. From A C we conclude that AC meets 1. From B* we conclude that BC meets 1. Now by Pasch's axiom (B4) it follows that AB does not meet 1. So A - B as required. V A D Case 2 Suppose A, B, C lie on a line m. As in Case 2 of the first part of the proof above, choose a point D on l, not on m, and use (B2) to get a point E with D* A * E. Then A - E as we showed above. Now, A * C by hypothesis, and A ~ E, so we conclude that C + E, since is an equivalence relation (if C ~ E, then A ~ by transitivity: contradiction). Looking at the three noncollinear points B, C, E, from E + C and B+C we conclude using Case 1 that B ~ E. But also A ~ E, so by transitivity, A ~ B as required. Proposition 7.2 (Line separation) Let A be a point on a line l. Then the set of points of l not equal to A can be divided into two nonempty subsets Si, S2, the two sides of A on l, such that (a) B, C are on the same side of A if and only if A is not in the segment BC; D C e (b) B, D are on opposite sides of A if and only if A belongs to the segment BD 'm E Proof Given the line l and a point A on 1, we know from (13) that there exists a point E not on l. Let m be the line con- taining A and E. Apply (7.1) to the line m. If m has two sides S, S, we define S and S2 to be the intersections of S and Sy with 1. Then properties (a) and (b) follow immediately from the previous proposition. A I 7. Axioms of Betweenness 77 The only mildly nontrivial part is to show that S and S2 are nonempty. By (12), there is a point B on l different from A. And by (B2) there exists a point D such that B * A * D. Then D will be on the opposite side of A from B, and will lie on l, so both sides are nonempty. Now that we have some basic results on betweenness, we can define rays and angles. A B B Definition Given two distinct points A, B, the ray AB is the set consisting of A, plus all points on the line AB that are on the same side of A as B. The point A is the origin, or vertex, of the ray. An angle is the union of two rays AB and AC originating at the same point, its vertex, and not lying on the same line. (Thus there is no "zero angle," and there is no "straight angle" (180).) Note that the vertex of a ray or angle is uniquely de- termined by the ray or angle (proof similar to Exercises 7.2, 7.3). The inside (or interior) of an angle BAC consists of all points D such that D and C are on the same side of the line AB, and D and B are on the same side of the line AC. If ABC is a triangle, the in- side (or interior) of the triangle ABC is the set of points that are simultaneously in the insides of the three angles LBAC, LABC, LACB. B B D Proposition 7.3 (Crossbar theorem) Let LBAC be an angle, and let D be a point in the interior of the angle. Then the ray AD must meet the segment BC. Proof This is similar to Pasch's axiom (B4), except that we must consider a line AD that passes through one vertex of the triangle ABC. We will prove it with Pasch's axiom and several applications of the plane separation theorem (7.1). D E A c Let us label the lines AB = 1, AC = m, AD = n. Let E be a point on m such 3 that E* A * C(B2). We will apply Pasch's axiom (B4) to the triangle BCE and the line n. By construction n meets the side CE at A. Also, n cannot contain B, be- cause it meets the line 1 at A. We will show that n does not meet the segment BE, so as to conclude by (B4) that it must meet the segment BC. So we consider the segment BE. This segment meets the line l only at B, so all points of the segment, except B, are on the same side of 1. By construction, is on the opposite side of 1 from E, so by (7.1) all points of BE, except B, are on the opposite side of 1 from C. On the other hand, since D is in the interior of the angle _BAC, all the points of the ray AD, except A, are on the same side of l as C. Thus the segment BE does not meet the ray AD. A similar reasoning using the line m shows that all points of the segment BE, except E, lie on the same side of m as B, while the points of the ray of n, opposite the ray AD, lie on the other side of m. Hence the segment BE cannot meet the opposite ray to AD. Together with the previous step, this shows that the seg- ment BE does not meet the line n. We conclude by (B4) that n meets the seg- ment BC in a point F. It remains only to show that F is on the ray AD of the line n. Indeed, B and Fare on the same side of m, and also B and D are on the same side of m, so (7.1) D and F are on the same side of m, and so D and F are on the same side of A on the line n. In other words, F lies on the ray AD