Discrete structure.

MD,

Please prepare the report according to the prompts in the project description, and submit it to eportfolio for peer review. Look forward to seeing your post and other's comments on your work.

______________________________________

#include

#include

using namespace std;

/* Fibonacci Series: recursive version */

int Fibonacci_Recursive(int n)

{

if(n

else if(n==1) return 1;

else return Fibonacci_Recursive(n-1)+Fibonacci_Recursive(n-2);

}

// Fibonacci Series: iterative version

int Fibonacci_Iterative(int n)

{

int fib[] = {0,1,1};

for(int i=2; i

{

fib[i%3] = fib[(i-1)%3] + fib[(i-2)%3];

//cout

}

return fib[n%3];

}

int main(void)

{

int n;

int long recursiveResult = 0;

int long iterativeresult = 0;

cout

cin>>n;

if(n

cout

return 0;

}

const long double sysTime = time(0);

const long double sysTimeMS = sysTime*1000;

cout

// calculate the fib(i) from scratch for each i

cout

cout

const long double endSysTime = time(0);

const long double endSysTimeMS = sysTime*1000;

cout

cout

// or calculate fib(a) once and output the intermediate results from the looping version

cout

cout

const long double end2SysTime = time(0);

const long double end2SysTimeMS = sysTime*1000;

cout

cout

return 0;

}

Description :

1. The above program is responsible for calculating Nth Fibonacci series number using both the techniques like recursive as well as iterative.

2. the above program caters following functinalities

A. Write an iterative C++ function that inputs a nonnegative integer n and returns the nth Fibonacci number.

B. Write a recursive C++ function that inputs a nonnegative integer n and returns the nth Fibonacci number.

Question 3: Compare the number of operations and time taken to compute Fibonacci numbers recursively versus that needed to compute them iteratively.

Answer : i have perfromed the testing of above program by taking maximum number and i found that when take n = 40 then it seems that recursive fuction is working find and gives the result but when i increase the value of n to 40+ or 50 , 60 , 80 and 100 above then the process takes too much time to calculate it so the nth number of series will become too large to supprort data types.Following output i got when i executed above program with n = 40 and 50

Output

----------

[https://d2vlcm61l7u1fs.cloudfront.net/media%2F14d%2F14dd9dec-d23b-40a0-8149-afb73bcdd0ea%2FphprZ6qPL.png]

n = 50 will take too much times to perform the operation in case of recursive technique where as iin case of iterative technique, it will perform operation very fast.

4. Use the above functions to write a C++ program for solving each of the following computational problems.

I. Find the exact value of f100, f500, and f1000, where fn is the nth Fibonacci number. What are times taken to find out the exact values?

II. Find the smallest Fibonacci number (1) greater than 1,000,000, and (2) greater than 1,000,000,000. I. Find the exact value of f100, f500, and f1000, where fn is the nth Fibonacci number. What are times taken to find out the exact values?

Answer :

f100 = 3736710778780434371 Iterative approch done 1492259751000 ms.

f500 = 2171430676560690477 Iterative approch done 1492259780000 ms

f1000 = 817770325994397771 Iterative approch done 1492259800000 ms

Time difference = f500 - f100 = 29000 ms or 29 sec

Time difference = f100 - f500 = 1492259800000 - 1492259780000 = 20000ms

II. Find the smallest Fibonacci number (1) greater than 1,000,000, and (2) greater than 1,000,000,000.

31th element in series would be greater than 1,000,000 - 1346269

45th element in series would be greater than 1,000,000,000 - 1134903170

Note : in above code just take long long datat type instead of int and you can get any nth number in series.

i.e long long Fibonacci_Iterative(int n)

2.

First I used the iteration function to find the Fibonacci numbers. Then I switched to recursion function. By doing this assignment I learn to use my skills from my previous classes. Fibocani number is closely connect with nature , science and real life. It is widely used in many fields and well-worth people exploring. For writing the code is taking me a long. Otherwise it is fun.

// // Another easy way to do it,

Iterative Method:

fib.cpp

#include

int calculateFibonacci(int n)

{

int a = 0, b = 1, c, i;

if( n == 0)

return a;

for (i = 2; i

{

c = a + b;

a = b;

b = c;

}

return b;

}

int main ()

{

// Trying to find the 9th Fibonacci number.

int n = 9;

std::cout

return 0;

}

$g++ fib.cpp

$./a.out

9th Fibonacci number is: 34

Recursive Approach:

fibRec.cpp

#include

int calculateFibonacci(int n)

{

if (n

return n;

return calculateFibonacci(n-1) + calculateFibonacci(n-2);

}

int main ()

{

int n = 9;

std::cout

return 0;

}

$g++ fib.cpp

$./a.out

9th Fibonacci number is: 34

/// Here is the modified solution...

#include

#include

using namespace std;

/* Fibonacci Series: recursive version */

int Fibonacci_Recursive(int n)

{

if(n

else if(n==1) return 1;

else return Fibonacci_Recursive(n-1)+Fibonacci_Recursive(n-2);

}

// Fibonacci Series: iterative version

int Fibonacci_Iterative(int n)

{

int fib[] = {0,1,1};

for(int i=2; i

{

fib[i%3] = fib[(i-1)%3] + fib[(i-2)%3];

//cout

}

return fib[n%3];

}

int main(void)

{

int n;

int long recursiveResult = 0;

int long iterativeresult = 0;

cout

cin>>n;

if(n

cout

return 0;

}

const long double sysTime = time(0);

const long double sysTimeMS = sysTime*1000;

cout

// calculate the fib(i) from scratch for each i

const clock_t startRecursive = clock();

cout

const clock_t endRecursive = clock();

cout

cout

const clock_t startIterative = clock();

// or calculate fib(a) once and output the intermediate results from the looping version

cout

const clock_t endIterative = clock();

cout

cout

cout

return 0;

}

Can someone do no. 2 for me please. Thank you

ASAP

okay,, so the question is......

MAC281 Discrete Structures Project (Integrative learning, written) Goal: The main goal of the project is to let students use their prior knowledge, try to use the skills they have learnt to solve real world problems. Using this assignment students are required to learn to use the skills they have learned in their previous classes, solve the problems given and reflect on how they can apply it to solve real world issues. Deliverables: The students are required to submit a written report along with the programs they have written. The report has to address all the prompts mentioned. The report should be properly presented by using appropriate font (Time new roman, preferably font size 12). Please keep the report ANONYMOUS without adding any name or course information. Tasks: 1. Write an iterative C++ function that inputs a nonnegative integer n and returns the nth Fibonacci number. 2. Write a recursive C++ function that inputs a nonnegative integer n and returns the nth Fibonacci number. 3. Compare the number of operations and time taken to compute Fibonacci numbers recursively versus that needed to compute them iteratively. 4. Use the above functions to write a C++ program for solving each of the following computational problems. I. Find the exact value of f100, f500, and f1000, where fn is the nth Fibonacci number. What are times taken to find out the exact values? II. Find the smallest Fibonacci number (1) greater than 1,000,000, and (2) greater than 1,000,000,000. III. Find as many prime Fibonacci numbers as you can. It is unknown whether there are infinitely many of these. Find out the times taken to find first 10, 20, 30, 40up to 200 and draw a graph and see the pattern. Initial report submission to Discussions, due on Sunday April 16: 1. Prepare a project report in WORD document to describe how you implement above tasks, including (1) problem analysis and solution plan, (2) source code, (3) discussion on experimental results in tables or graphs, (4) reflection and conclusion. 2. Your reflection should address all of the below mentioned questions a) Describe the Fibonacci series and write briefly what you have done in the assignment. b) What are the different skills, programming techniques have you used in order to run the experiments? c) What did you observe when you did the comparisons in Task 3 and Task 4? Explain the graph that you have drawn from Task 4.III? d) List at least three different applications of the Fibonacci numbers to sciences and describe one of them in details. Think of situation or a real world problem where you can apply concept of Fibonacci numbers to solve it. Explain? e) Write a paragraph, explaining what you have done in this assignment. What were the challenges you have faced when solving these problems. How can you improve the programs you have written to solve these problems? so...i get this answer so far,, but i need no... 2,,,, still,, i

#include #include

using namespace std;

/* Fibonacci Series: recursive version */ int Fibonacci_Recursive(int n) { if(n

// Fibonacci Series: iterative version int Fibonacci_Iterative(int n) { int fib[] = {0,1,1}; for(int i=2; i

int main(void) { int n; int long recursiveResult = 0; int long iterativeresult = 0; cout >n; if(n

const long double endSysTime = time(0); const long double endSysTimeMS = sysTime*1000; cout

// or calculate fib(a) once and output the intermediate results from the looping version cout

Description :

1. The above program is responsible for calculating Nth Fibonacci series number using both the techniques like recursive as well as iterative.

2. the above program caters following functinalities

A. Write an iterative C++ function that inputs a nonnegative integer n and returns the nth Fibonacci number.

B. Write a recursive C++ function that inputs a nonnegative integer n and returns the nth Fibonacci number.

Question 3: Compare the number of operations and time taken to compute Fibonacci numbers recursively versus that needed to compute them iteratively.

Answer : i have perfromed the testing of above program by taking maximum number and i found that when take n = 40 then it seems that recursive fuction is working find and gives the result but when i increase the value of n to 40+ or 50 , 60 , 80 and 100 above then the process takes too much time to calculate it so the nth number of series will become too large to supprort data types.Following output i got when i executed above program with n = 40 and 50

Output

----------

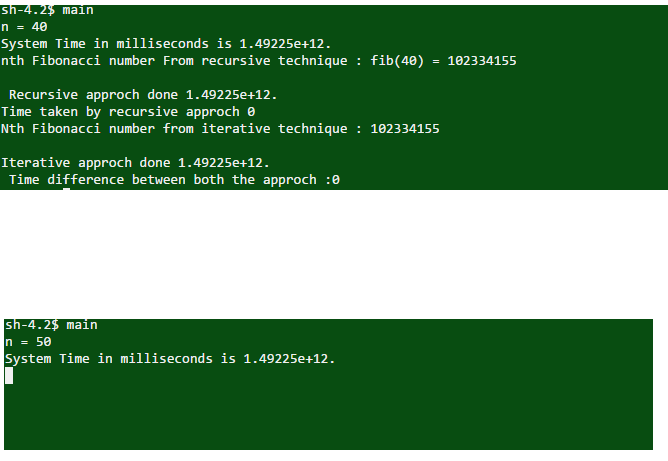
n = 50 will take too much times to perform the operation in case of recursive technique where as iin case of iterative technique, it will perform operation very fast.

4. Use the above functions to write a C++ program for solving each of the following computational problems. I. Find the exact value of f100, f500, and f1000, where fn is the nth Fibonacci number. What are times taken to find out the exact values? II. Find the smallest Fibonacci number (1) greater than 1,000,000, and (2) greater than 1,000,000,000. I. Find the exact value of f100, f500, and f1000, where fn is the nth Fibonacci number. What are times taken to find out the exact values?

Answer :

f100 = 3736710778780434371 Iterative approch done 1492259751000 ms. f500 = 2171430676560690477 Iterative approch done 1492259780000 ms f1000 = 817770325994397771 Iterative approch done 1492259800000 ms

Time difference = f500 - f100 = 29000 ms or 29 sec Time difference = f100 - f500 = 1492259800000 - 1492259780000 = 20000ms

II. Find the smallest Fibonacci number (1) greater than 1,000,000, and (2) greater than 1,000,000,000.

31th element in series would be greater than 1,000,000 - 1346269 45th element in series would be greater than 1,000,000,000 - 1134903170

Note : in above code just take long long datat type instead of int and you can get any nth number in series.

i.e long long Fibonacci_Iterative(int n)

need more more description

main System Time in milliseconds is 1.49225e+12. nth Fibonacci number From recursive technique fib(40) 102334155 Recursive approch done 1.49225e+12. Time taken by recursive approch 0 Nth Fibonacci number from iterative technique 102334155 Iterative approch done 1.4 Time difference between both the approch :0 4.2$ main 50 System Time in milliseconds is 1.49225e+12 main System Time in milliseconds is 1.49225e+12. nth Fibonacci number From recursive technique fib(40) 102334155 Recursive approch done 1.49225e+12. Time taken by recursive approch 0 Nth Fibonacci number from iterative technique 102334155 Iterative approch done 1.4 Time difference between both the approch :0 4.2$ main 50 System Time in milliseconds is 1.49225e+12