Do number 2 and 3 the sas output part has been done already.
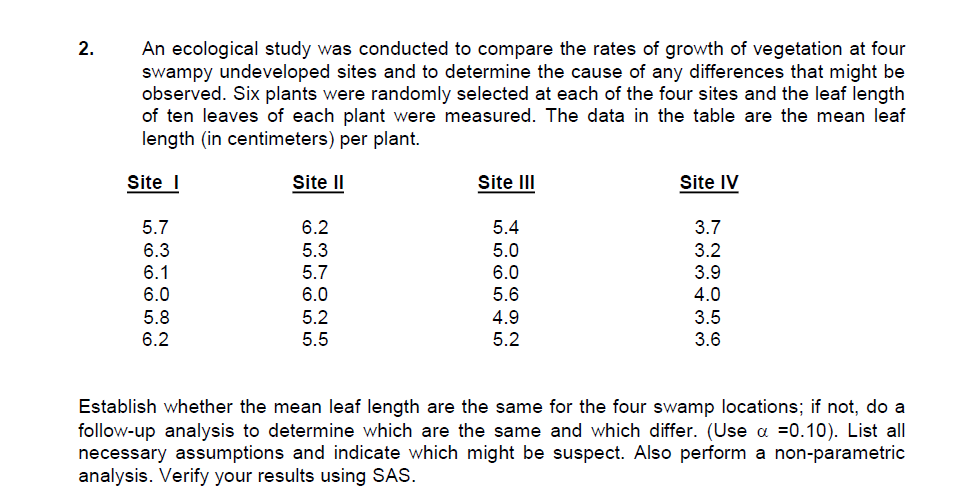
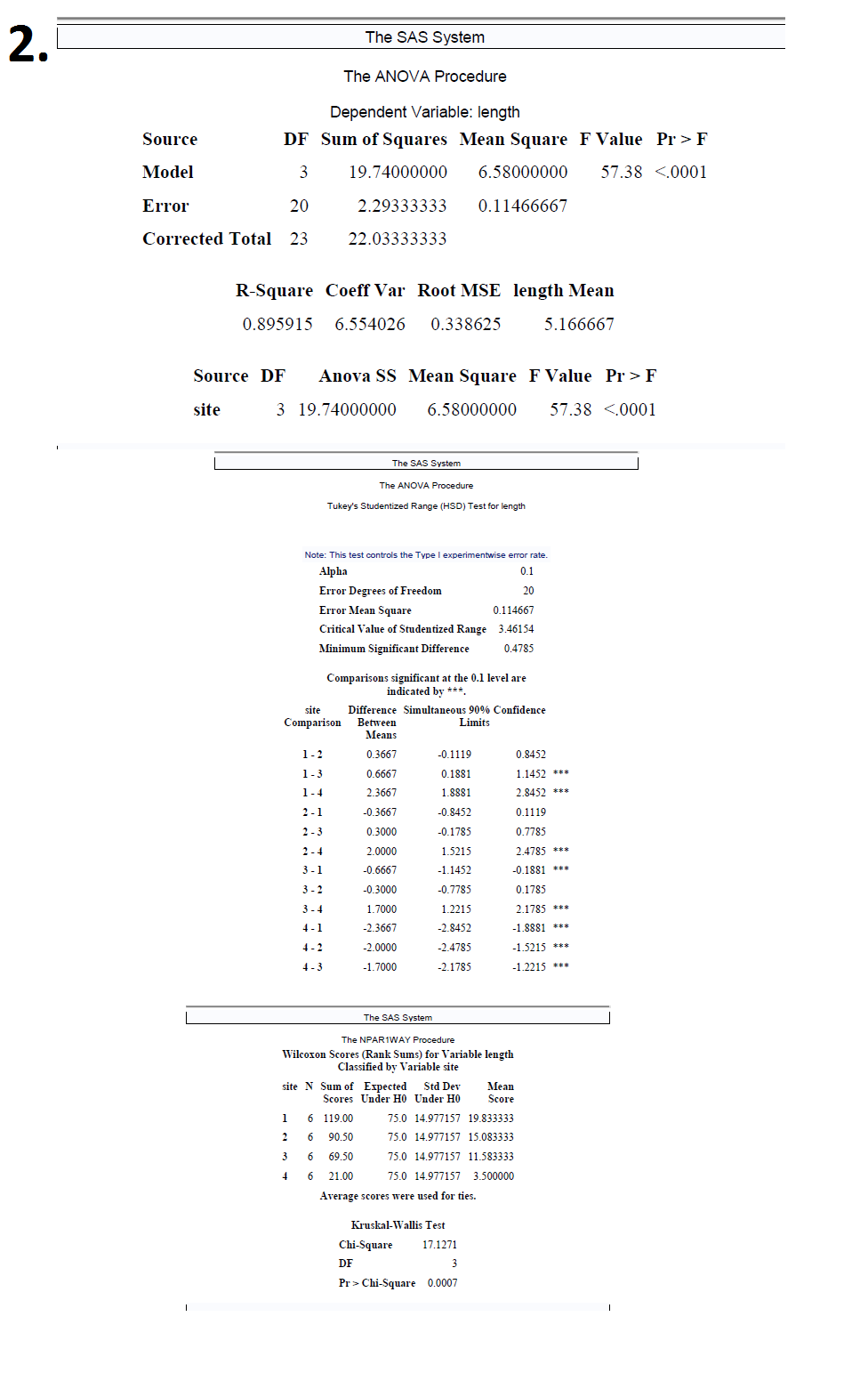
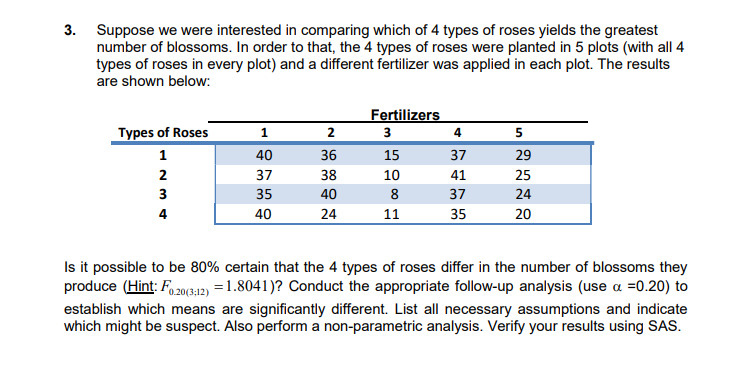
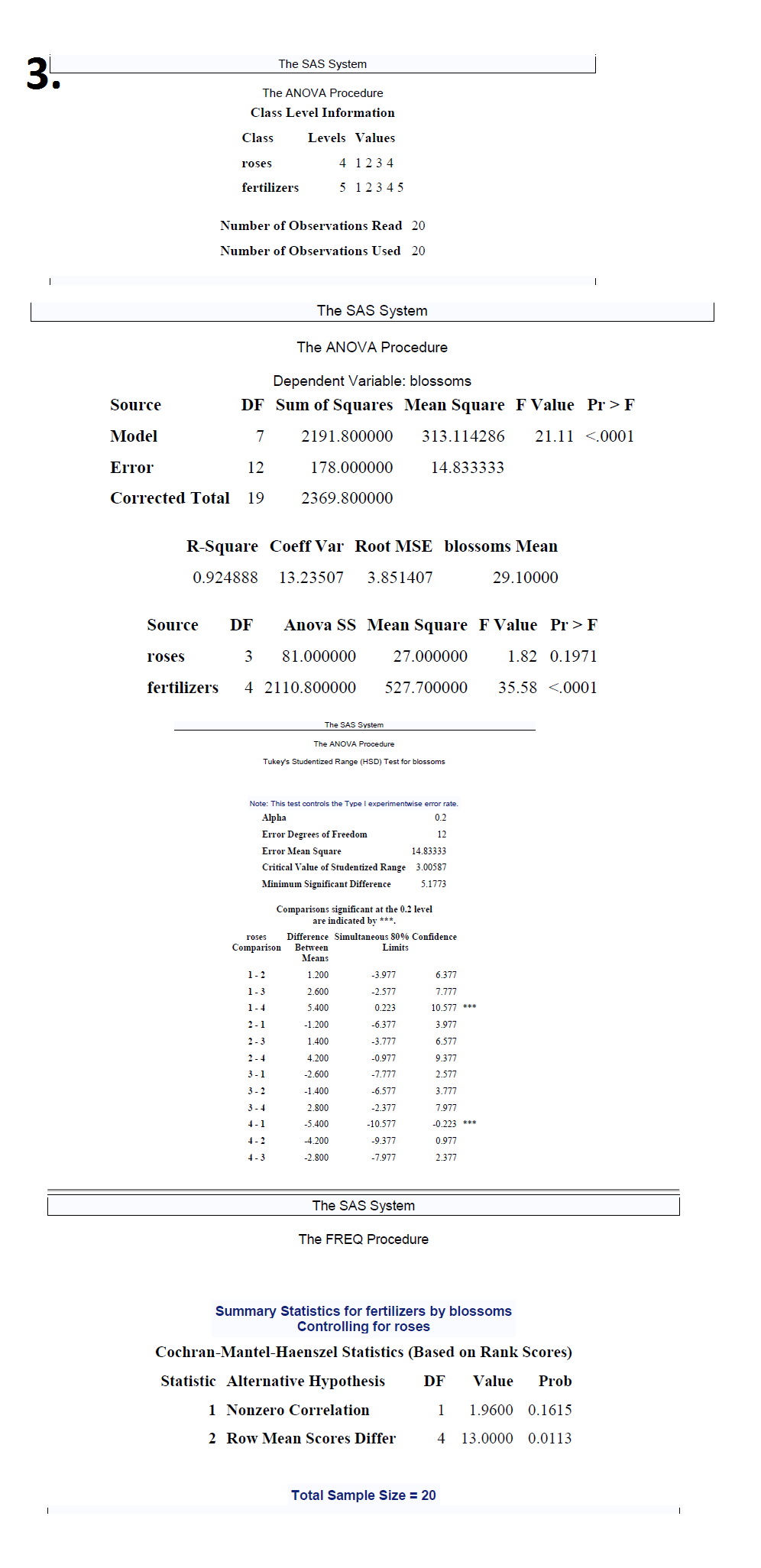
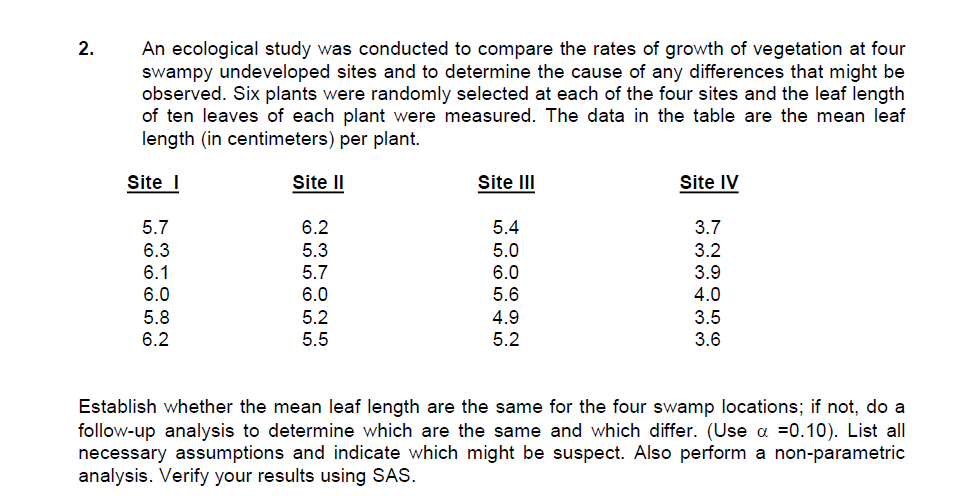
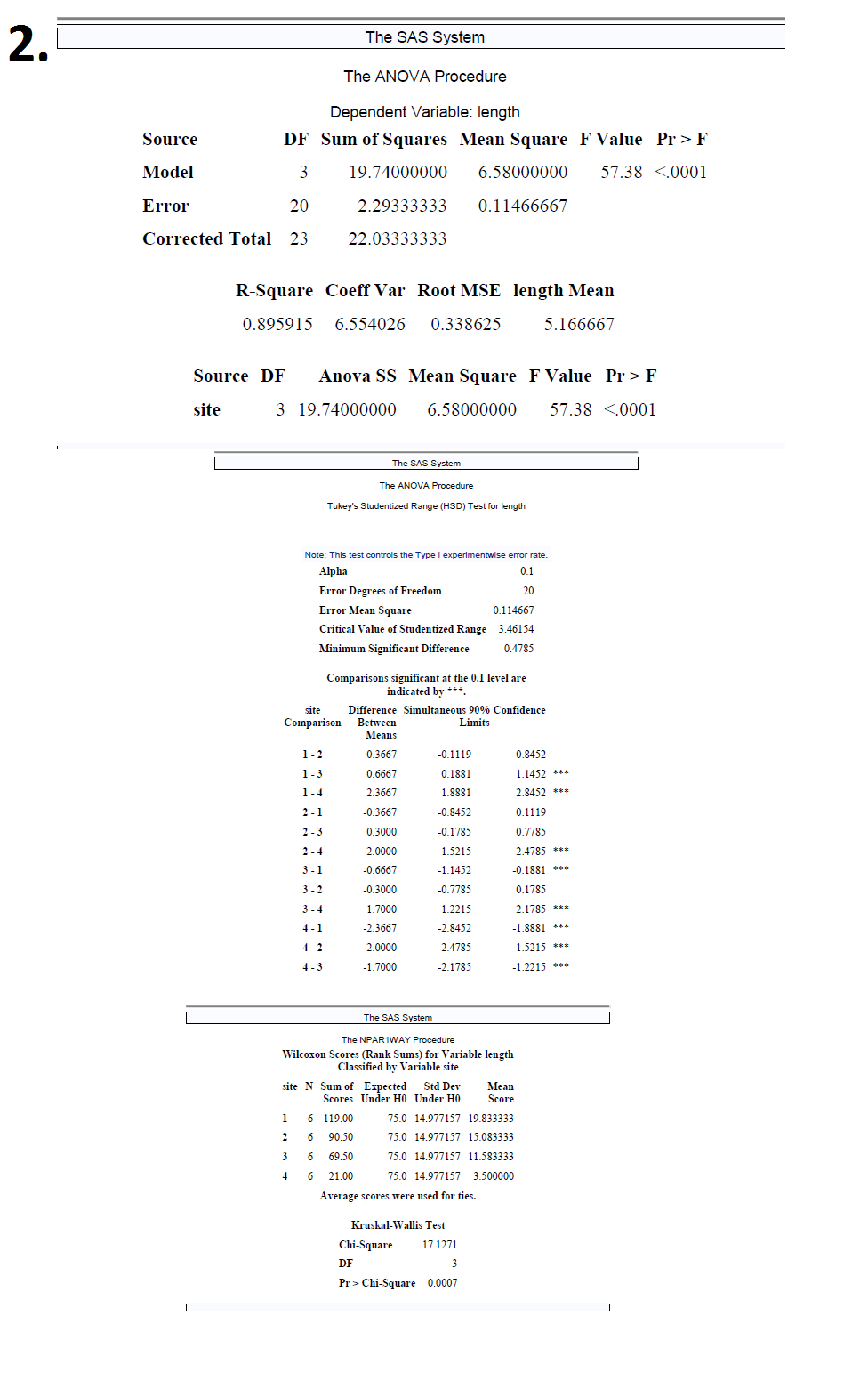
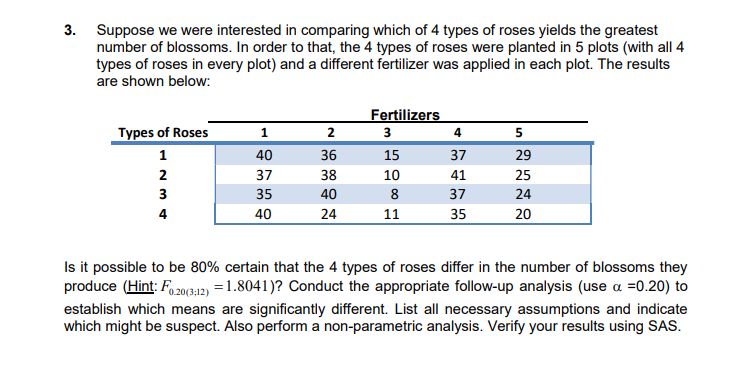
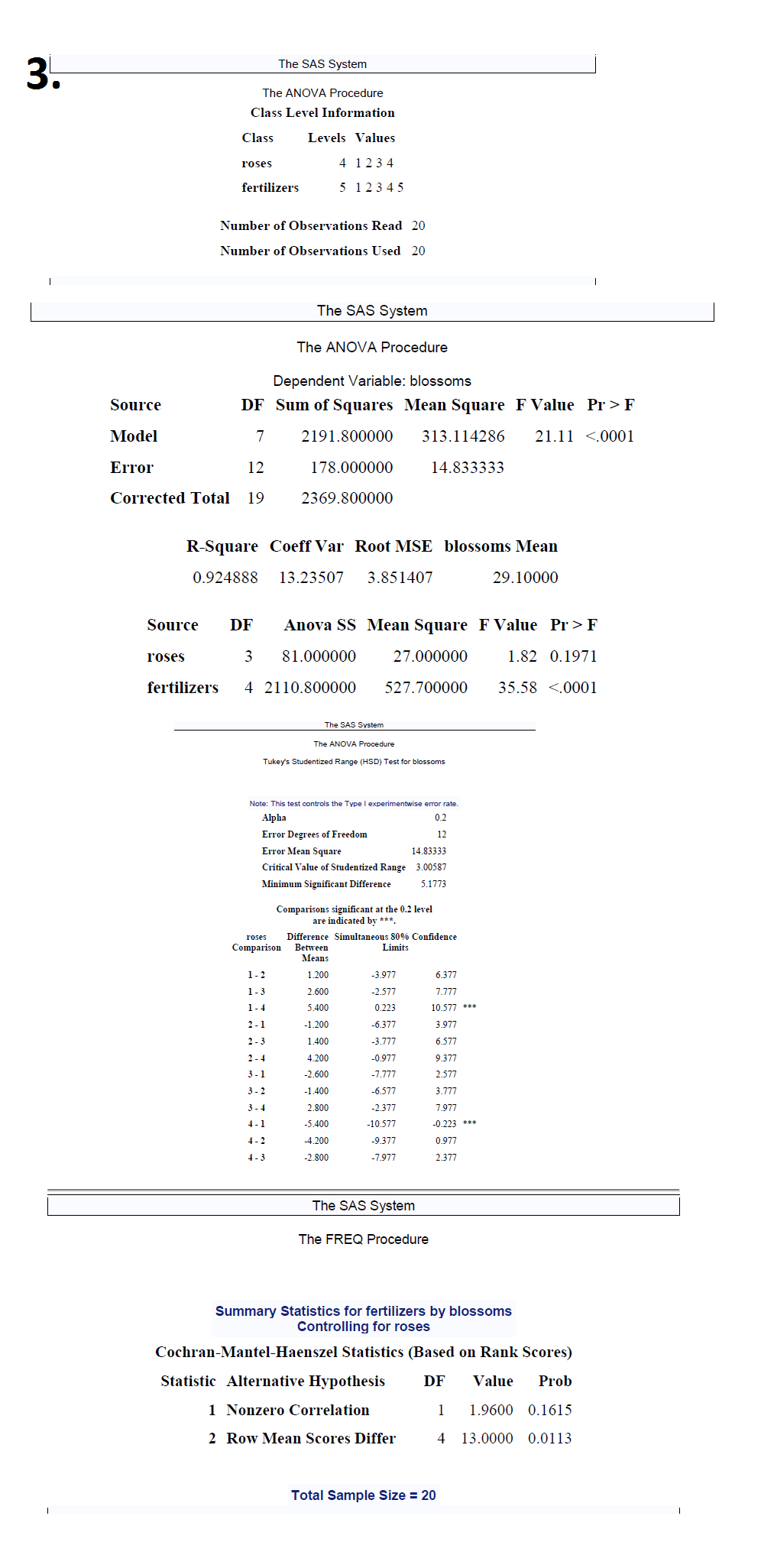
2. An ecological study was conducted to compare the rates of growth of vegetation at four swampy undeveloped sites and to determine the cause of any differences that might be observed. Six plants were randomly selected at each of the four sites and the leaf length of ten leaves of each plant were measured. The data in the table are the mean leaf length (in centimeters) per plant. Site I Site II Site III Site IV 5.7 6.2 5.4 3.7 6.3 5.3 5.0 3.2 6.1 5.7 6.0 3.9 6.0 6.0 5.6 4.0 5.8 5.2 4.9 3.5 6.2 5.5 5.2 3.6 Establish whether the mean leaf length are the same for the four swamp locations; if not, do a follow-up analysis to determine which are the same and which differ. (Use {1 =0.10). List all necessary assumptions and indicate which might be suspect. Also perform a non-parametric analysis. Verify your results using SAS. 2. The SAS System The ANOVA Procedure Dependent Variable: length Source DF Sum of Squares Mean Square F Value Pr > F Model 19.74000000 6.58000000 57.38 <.0001 error corrected total r-square coeff var root mse length mean source df anova ss square f value pr> F site 3 19.74000000 6.58000000 57.38 <.0001 the sas system anova procedure tukey studentized range test for length note: this controls type i experimentwise error rate alpha degrees of freedom mean square critical value minimum significant difference comparisons at level are indicated by site simultaneous confidence comparison between limits means npar1way wilcoxon scores sums variable classified n sum expected std dev under ho mea score average were used ties. kruskal-wallis chi-square df pr> Chi-Square 0.00073 . Suppose we were interested in comparing which of 4 types of roses yields the greatest number of blossoms In order to that the 4 types of roses were planted in 5 plots ( with all 4 types of roses in every plot ) and a different fertilizer was applied in each plot The results are shown below : Fertilizers Types of Roses 40 36 15 37 29 37 38 10 41 25 35 40 37 24 40 24 11 35 20 Is it possible to be 80% certain that the 4 types of roses differ in the number of blossoms they produce ( Hint : Function , = 1 8041 ) ? Conduct the appropriate follow- up analysis ( use a = 0 . 20 ) to establish which means are significantly different List all necessary assumptions and indicate which might be suspect Also perform a non -parametric analysis . Verify your results using SAS3. The SAS System The ANOVA Procedure Class Level Information Class Levels Values roses 4 123 4 fertilizers 5 12345 Number of Observations Read 20 Number of Observations Used 20 The SAS System The ANOVA Procedure Dependent Variable: blossoms Source DF Sum of Squares Mean Square F Value Pr > F Model 2191.800000 313.114286 21.11 <.0001 error corrected total r-square coeff var root mse blossoms mean source df anova ss square f value pr> F rose 81.000000 27.000000 1.82 0.1971 fertilizers 4 2110.800000 527.700000 35.58 <.0001 the sas system anova procedure tukey studentized range test for blossoms note: this controls type i experimentwise error rate alpha degrees of freedom mean square critical value minimum significant difference comparisons at level are indicated by roses simultaneous confidence comparison between limits means freq summary statistics fertilizers controlling cochran-mantel-haenszel on rank scores statistic alternative hypothesis df prob nonzero correlation row differ total sample size="20">