Draw Cash Flow Diagram Of the Given Solutions

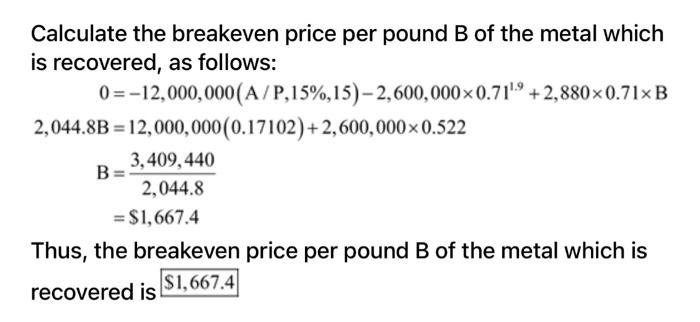
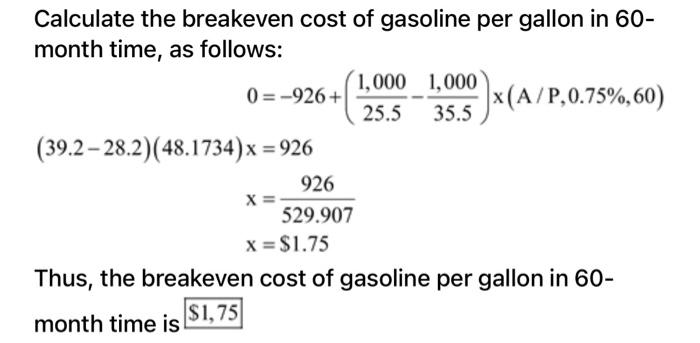
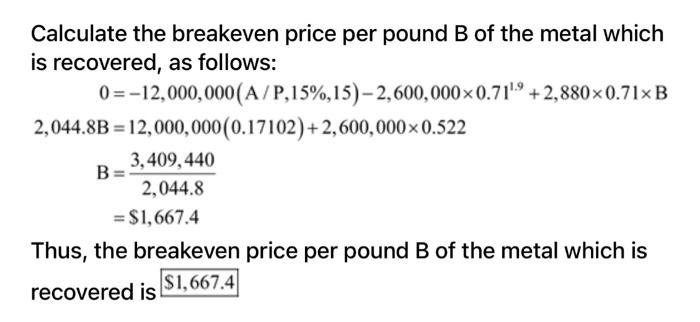
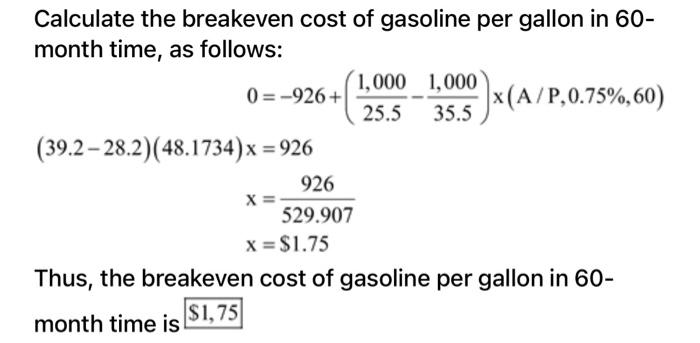
Draw the diagram of just first four parts

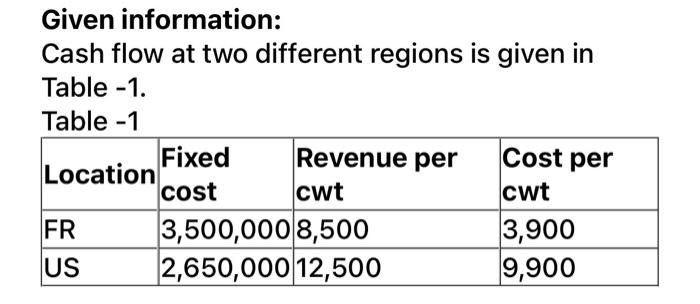
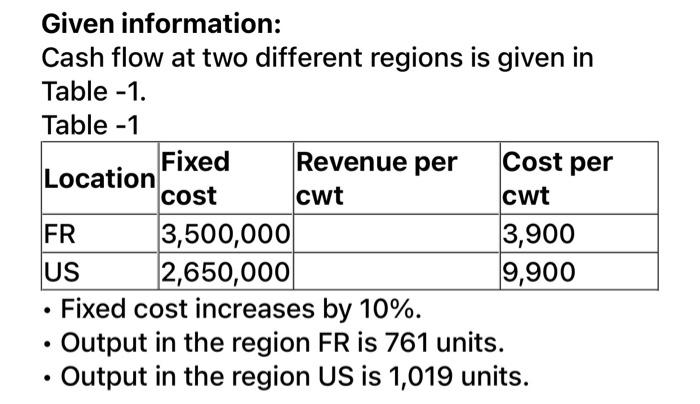
(a) Here r is $589 and v is $340, breakeven quantity is 9000. The fixed cost will be FC 9000 = 589-340 FC = 9000 x 249 FC = $2,241,000 Thus, the fixed cost is $2,241,000 per year. (b) Here Q is 7000, FC is $750,000, ris $589 and v is $340. The profit will be P= 589x 7000-(750000+ 340x 7000) P=589x 7000-(750000+ 340 x 7000) P = $993,000 Thus, the profit is $993,000 per year. (a) Calculate the breakeven quantity Q as follows: FC Q= P-VC 800,000 2,950 - 2,075 =914 Thus, the breakeven quantity is 914 (b) Calculate the profit when 3,000 units are sold as follows: Pr = (P-VC)Q-FC = (2,950 - 2,075)3,000-800,000 = 2,625,000 - 800,000 = $1,825,000 Thus, the profit when 3,000 units are sold is $1,825,000 Calculate the breakeven price per pound B of the metal which is recovered, as follows: 0=-12,000,000(A/P,15%,15) 2,600,000x0.71'9 +2,880x0.71XB 2,044.8B = 12,000,000(0.17102)+2,600,000x0.522 3,409,440 B 2,044.8 = $1,667.4 Thus, the breakeven price per pound B of the metal which is recovered is $1,667.4 Given information: Cash flow at two different regions is given in Table - 1. . Table - 1 Fixed Revenue per Location cost cwt cwt FR 3,500,000 8,500 3,900 US 2,650,000 12,500 9,900 Cost per - Breakeven point units in the region FR: Breakeven point can be calculated as follows: Fixed cost Breakeven point units Revenue per unit - Cost per unit 3,500,000 8,500 - 3,900 3,500,000 4,600 = 760.87 Thus, breakeven point unit for the region FR is 761 Breakeven point units in the region US: Breakeven point can be calculated as follows: Fixed cost Breakeven point units Revenue per unit - Cost per unit 2,650,000 12,500-9,900 2,650,000 2,600 = 1,019.23 Thus, breakeven point unit for the region US is 1,019 Given information: Cash flow at two different regions is given in Table - 1. Table - 1 Fixed Revenue per Cost per Location cost cwt cwt FR 3,500,000 3,900 US 2,650,000 9,900 Fixed cost increases by 10%. Output in the region FR is 761 units. Output in the region US is 1,019 units. . Breakeven point revenue per unit in the region FR: Breakeven point revenue per unit can be calculated as follows: Fixed cost (1+ Increasing percent of fxed cost) Breakeven point revenue per unit = Break even pint unir +Cost per unit 3,500,000 (1 +0.1) +3,900 761 3,850,000 +3,900 761 = 5,059.13+3,900 = 8,959.13 Thus, breakeven point revenue per unit in the region FR is $8,959.131 Breakeven point revenue per unit in the region US: Breakeven point can be calculated as follows: Fixed cost (1+ Increasing percent of fxed cost) Breakeven point units = Break even pint unir +Cost per unit 2,650,000(1.1) +9,900 1,019 2,915,000 +9,900 1,019 = 2,860.65 +9,900 = 12,760.65 Thus, breakeven point revenue per unit in the region US is $12, 760.65 Calculate the profit of F plant when 950 units are sold as follows: Pr = (P-VC)Q-FC =(8,500 3,900)950 3,500,000 = 4,370,000 -3,500,000 = $870,000 Thus, the profit of F plant when 950 units are sold is $870,000 Calculate the profit of U plant when 850 units are sold as follows: Pr =(P-VC)Q-FC = (12,500 - 9,900)850 2,650,000 = 2,210,000 - 2,650,000 = $-440,000 Thus, the profit of U plant when 950 units are sold is $ - 440,000 = Enterprises want to raise profit by $ 1 million without change in revenue and fixed cost, calculate the decrease in currency amount in and increase in variable cost For Country F Profit=Total revenue - Total cost 1,000,000 8500(950) -3,500,000 - v(950) 8,075,000-3,500,000-1,000,000 Variable cost = 950 3,575,000 950 = 3,763.15789 change in variable cost=3,900-3763.158 = 136.82 136.842 % change in variable cost=. x 100 3900 = 3.5% Thus, the variable cost should be drop by 3.5% to achieve $1 million profit in Country F For U.S. Profit=Total revenue - Total cost 1,000,000 = 12,500(850) 2,650,000 - v(850) Variable cost = 10,625,000 -2,650,000 - 1,000,000 850 = 8205.88 change in variable cost=9,900-8,205 =1,695 1695 % change in variable cost= -x100 9900 = 17.11% Thus, the variable cost should be drop by 11.7% to achieve $1 million profit in U.S. Calculate the breakeven cost of gasoline per gallon in 60- month time, as follows: 1,000 1,000 0= -926+ x(A/P,0.75%,60) 25.5 35.5 (39.2 28.2)(48.1734)x = 926 926 529.907 X = $1.75 Thus, the breakeven cost of gasoline per gallon in 60- month time is $1,75 (a) Calculate the breakeven quantity Q as follows: FC Q= P-VC 775,000 2.50-1 = 516,667 Calculate the breakeven quantity as percentage of total capacity, as follows: 516,667 Percent = x 100 1,400,000 = 37% Thus, the breakeven quantity as percentage of total capacity is 37% (b) Calculate the required revenue R as follows: FC Q= P-VC 50%~900,000 500,000 = R-1 500,000R - 500,000 = 450,000 950,000 R= 500,000 = $1.9 So, the new product call rate is $0.6 less than current center revenue. Calculate the breakeven miles that should be traveled every month, as follows: 3.25 3.25 0 = -800+ x(P/A,1%,36) 18 21 (0.0258)(30.1075)X = 926 800 X= 0.7768 X = 1,030 Thus, the breakeven miles that should be traveled 1,030 every month is