Question
Dr.Racket (Intermediate Student with lambda Language) ------------------------------------------------------------------------------------------------------------------------- One branch of computing that is very concerned with the kind ofsearch we've beenstudying is Artificial Intelligence (AI).
Dr.Racket (Intermediate Student with lambda Language)
-------------------------------------------------------------------------------------------------------------------------
One branch of computing that is very concerned with the kind ofsearch we've beenstudying is Artificial Intelligence (AI).
In AI, the "planning" problem is when you are given:+ a description (list of facts) of the current "state" of theworld+ a description of the state you'd like it to be (the "goal")+ a set of actions that you can perform
Each action has:+ requirements needed in the current state before you can take thataction+ a list of facts removed from the current state when the action istaken+ a list of facts added to the current state when the action istaken
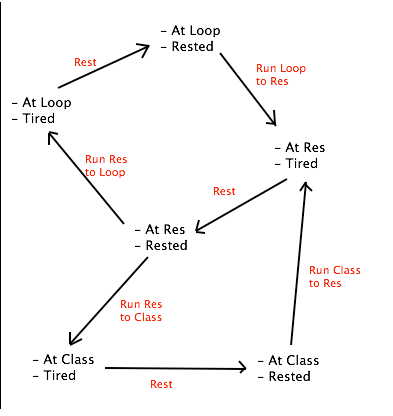
FOR EXAMPLE: Suppose that our planning problem is that we are atthe bus loopand would like to go to class. But there are only five possibleactions that we can take: 1. "Run Loop to Res" 2. "Run Res to Loop" 3. "Run Res to Class" 4. "Run Class to Res" 5. "Rest"
If we look closely at one action, say "Run Loop to Res" (seebelow), we will find that:+ The requirements for this action are: "At Loop" and "Rested" (how am I supposed to run otherwise?)+ The facts removed from the current state: "At Loop" and"Rested"+ The facts added to current state: "At Res" and "Tired"
Using our example, the current state is: "At Loop" and"Rested"The goal state is: "At Class"
Although there are 5 UBC actions (below), we only want toconsider the actions that arepossible given the current state (whose requirements match ourcurrent state).
At our current state, only one action is possible: "Run Loop toRes"
If we take that action, then this is our current state: "At Res" and "Tired"
From here, we again find that we can only take one action:"Rest"
Which gets us to this state: "At Res" and "Rested"
At this point, two actions are possible: "Run Res to Loop" "Run Res to Class"
You may also note that this problem has a strange property where wecan return to previousstates. For example, we can run from the Bus Loop to Res backto the Bus Loop - even thoughthis is not productive! That means we are searching over a graph,and you'll have to handlethat in your program.
So any function you design to search the generated graph of statesis going to have to doavoid cycles, and should also avoid working on a node twice ifthere are two paths to it.
WE WANT YOU TO DESIGN TWO FUNCTIONS
- One function called solvable?, that consumes a startstate, a goal state and a list of actions and produces true if it is possible toreach the goal from the start using the given actions.
- A second more sophisticated function called solve, thatconsumes a start state, a goal state and a list of actions, and if it is possible toreach the goal produces the list of action names required. If it is not possible itproduces false.
Both functions must be tail recursive. The second functionis noticeably harder.
We have provided you with a number of things to give you a headstart: - signature, purpose and some tests for the two functionsyou need to design - data definitions for states and actions - a template for searching an arbitrary-arity tree ofstates - some hints about working with that template - a few other useful functions
We have also provided the signature, purpose, a stub, andcheck-expects for the solve function.You will need to complete the solve function by writing the originof template statement, andfinishing the function body. You will also need to design helperfunctions for solve. We haveprovided the full design of several (but not ALL) of these helperfunctions.
;; ============ DATA DEFINITIONS
;; State is (listof String);; interp. a state of the world, consisting of true;; facts as strings. Should not containrepeats!(define STATE-EMPTY empty)
; Running around UBC states:(define STATE-AT-LOOP-RESTED (list "At Loop" "Rested"))(define STATE-AT-CLASS-RESTED (list "At Class" "Rested"))(define STATE-AT-RES (list "AtRes" ))
#;(define (fn-for-state s) (cond [(empty? s) ...] [else (... (first s) (fn-for-state(rest s)))]))
(define-struct act (name pre del add));; Action is (make-act String (listof String) (listof String)(listof String));; interp. an action we can take, which requires all thepreconditions;; (pre) to be true in the state toperform and which--if taken--removes;; any deletions (del) that are in thestate and adds any results (add);; not already in the state
; Running around UBC actions:(define ACT-RUN-A-B (make-act "Run Loop to Res" (list "At Loop""Rested") (list "At Loop""Rested") (list "At Res""Tired")))(define ACT-RUN-B-A (make-act "Run Res to Loop" (list "At Res""Rested") (list "At Res""Rested") (list "At Loop""Tired")))(define ACT-RUN-B-C (make-act "Run Res to Class" (list "At Res""Rested") (list "At Res""Rested") (list "At Class""Tired")))(define ACT-RUN-C-B (make-act "Run Class to Res" (list "At Class""Rested") (list "At Class""Rested") (list "At Res""Tired")))(define ACT-REST (make-act "Rest" (list) (list "Tired") (list "Rested")))
#;(define (fn-for-action a) (... (act-name a) (fn-for-los (act-pre a)) (fn-for-los (act-del a)) (fn-for-los (act-add a))))
; Running around UBC problems:(define UBC-ACTIONS (list ACT-RUN-A-B ACT-RUN-B-A ACT-RUN-B-CACT-RUN-C-B ACT-REST))
;; ============ FUNCTIONS
;; Here is the FIRST step of templating a search over agenerated graph of States.;; Note that all this does is the generated tree of states. Notealso that in this;; template s is a State, and los is a (listof State). los isNOT a (listof String).;; Try to avoid remembing that State is (listof String) during thedevelopment of;; your main backtracking search functions. The helpers arethe ones that will need;; to know that State is (listof String);;;; You will still have lots to add to this template, like worklistsand other accumulators.
;; #;(define (fn-for-aat-of-state s0) (local [(define (fn-for-state s) (cond [(trivial? s)(trivial-answer s)] [else (fn-for-los (next-states s))])) (define (fn-for-los los) (cond [(empty? los)(...)] [else (... (fn-for-state (first los)) (fn-for-los (rest los)))]))] (fn-for-state s0)))
;; State State (listof Action) -> Boolean;; produce true if it is possible to reach goal, starting at s,with the given actions(check-expect (solveable? STATE-AT-LOOP-RESTEDSTATE-AT-CLASS-RESTED UBC-ACTIONS) true)
(check-expect (solveable? STATE-AT-LOOP-RESTED STATE-AT-RES UBC-ACTIONS) true)
(check-expect (solveable? STATE-AT-LOOP-RESTED (list "FOMO: AtICCS") UBC-ACTIONS) false)
(define (solveable? s goal actions) false)
;; State State (listof Action) -> (listof String) orfalse;; produce a list of action names that, taken together, will solvethe problem(check-expect (solve STATE-AT-LOOP-RESTED STATE-AT-CLASS-RESTEDUBC-ACTIONS) (list "Run Loop toRes" "Rest" "Run Res to Class" "Rest"))
(check-expect (solve STATE-AT-LOOP-RESTED STATE-AT-RES UBC-ACTIONS) (list "Run Loop toRes"))
(check-expect (solve STATE-AT-LOOP-RESTED (list "FOMO: At ICCS")UBC-ACTIONS) false)
(define (solve s goal actions) false)
;; State State -> Boolean;; produce true if s1 contains every element of s2 (but notnecessarily vice-versa)(check-expect (contains-all? (list "a" "b") (list "c")) false)(check-expect (contains-all? (list "a" "c") (list "c")) true)(check-expect (contains-all? (list "a" "c") (list "c" "d"))false)
;; (define (contains-all? s1 s2) (andmap (lambda (x2) (member x2 s1)) s2))
;; Action State -> State;; applies action to current state;; ASSUME: preconditions for action are already met(check-expect (apply-action-to-state ACT-RUN-A-B (list "At Loop""Rested")) (list "At Res""Tired"))
;;(define (apply-action-to-state a s) (foldr cons-if-not (foldr remove-all s (act-del a));should be ok to use remove (act-add a)))
;; X (listof X) -> (listof X);; cons x onto the front of lox unless it is already a member oflox(check-expect (cons-if-not "x" empty) (list "x"))(check-expect (cons-if-not "x" (list "x")) (list "x"))(check-expect (cons-if-not "x" (list "y" "x")) (list "y""x"))(check-expect (cons-if-not "x" (list "a" "b")) (list "x" "a""b"))
(define (cons-if-not x lox) (if (member? x lox) lox (cons x lox)))
- At Loop - Tired Rest Run Res to Loop - At Class - Tired - At Loop - Rested - At Res - Rested Run Res to Class Rest Rest Run Loop to Res - At Res - Tired Run Class to Res - At Class - Rested
Step by Step Solution
There are 3 Steps involved in it
Step: 1
To determine the number of teeth on all the wheels and the exact pitch circle diameter of A we can f...
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


