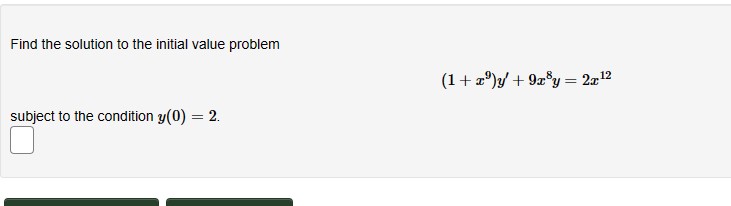
dy Solve the following differential equation. e2-3y and y = 1 when x = 0 da y Hint: Recognize this as a first-order linear differential equation and follow the general method for solving these and use the initial conditions to find the integration constant. Find the solution to the initial value problem (1+x)y' +9x8y = 2x12 subject to the condition y(0) = 2. A tank initially contains 200 gallons of brine, with 50 pounds of salt in solution. Brine containing 2 pounds of salt per gallon is entering the tank at the rate of 4 gallons per minute and is is flowing out at the same rate. If the mixture in the tank is kept uniform by constant stirring, find the amount of salt in the tank at the end of 40 minutes. The amount of salt in the tank at the end of 40 minutes is pounds. For this problem A is the amount of salt in the tank. If a tank contains 250 liters of liquid with 11 grams of salt. A mixture containing 10 grams per liter is pumped into the tank at a rate of 6 liters/minute. The mixture is well-mixed, and pumped out at a rate of 9 liters/minute. The amount of salt in the tank satisfies the differential equation = 0. Rewriting this as a linear differential equation we get = 60 The integrating factor is and the solution is