Each year, the U.S Naval Postgraduate School sets aside a 'Discovery Day' during which the general public is invited into their laboratories. Data below come from October 21, 1995, when visitor could test their motor learning and hand-eye coordination in the Human System Integration Laboratory. The variable of interest, 'contact time', comes from a rotary pursuit tracking experiment. A rotating sheet contains a 3/4 inch target spot which moves. The sheet is either in the shape of a circle or a square. The subject is asked to maintain contact with the moving target spot using a metal wand. Each trial lasted 15 seconds and the total contact time was recorded. The target spot moves keeps a constant speed in a circular path on the circle sheet, but moves at varying speeds in an irregular path on the square sheet.

Each of 108 visitors completed the trial four times but for only one of the two shapes (circle, square).

Age and Gender were also recorded. Visitors tended to come in family groups, but that information was not recorded.

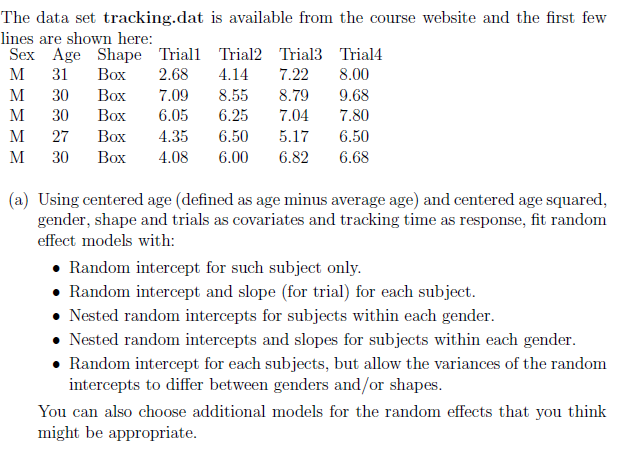
Data set is given as the example above. (Variables are 'Sex', 'Shape' (2 Categorical Data), 'Age', 'Trial1~4' (5 Numerical Data))

I wonder how to make a linear mixed random-effects model in r.

(such as lmer(formula = extro ~ open + agree + social + class + (1|school/class))

Could you suggest a number of example models to use for model analysis in r code?

Thanks.

The data set tracking.dat is available from the course website and the first few lines are shown here: Sex Age Shape Trial Trial2 Trial Trial4 M 31 Box 2.68 4.14 7.22 8.00 M 30 Box 7.09 8.55 8.79 9.68 M 30 Box 6.05 6.25 7.04 7.80 M 27 Box 4.35 6.50 5.17 6.50 M 30 Box 4.08 6.00 6.82 6.68 (a) Using centered age (defined as age minus average age) and centered age squared, gender, shape and trials as covariates and tracking time as response, fit random effect models with: Random intercept for such subject only. Random intercept and slope (for trial) for each subject. Nested random intercepts for subjects within each gender. Nested random intercepts and slopes for subjects within each gender. Random intercept for each subjects, but allow the variances of the random intercepts to differ between genders and/or shapes. You can also choose additional models for the random effects that you think might be appropriate. The data set tracking.dat is available from the course website and the first few lines are shown here: Sex Age Shape Trial Trial2 Trial Trial4 M 31 Box 2.68 4.14 7.22 8.00 M 30 Box 7.09 8.55 8.79 9.68 M 30 Box 6.05 6.25 7.04 7.80 M 27 Box 4.35 6.50 5.17 6.50 M 30 Box 4.08 6.00 6.82 6.68 (a) Using centered age (defined as age minus average age) and centered age squared, gender, shape and trials as covariates and tracking time as response, fit random effect models with: Random intercept for such subject only. Random intercept and slope (for trial) for each subject. Nested random intercepts for subjects within each gender. Nested random intercepts and slopes for subjects within each gender. Random intercept for each subjects, but allow the variances of the random intercepts to differ between genders and/or shapes. You can also choose additional models for the random effects that you think might be appropriate