Ed owns a small business called Kingston Anchors, which produces four types of anchor for pleasure craft:

Danforth: a lightweight, temporary anchor;

Small Plow: an all purpose anchor for boats less than 24';

Large Plow: same thing for boats longer than 24';

Hereshoff: a fancy, show-off anchor for larger boats.

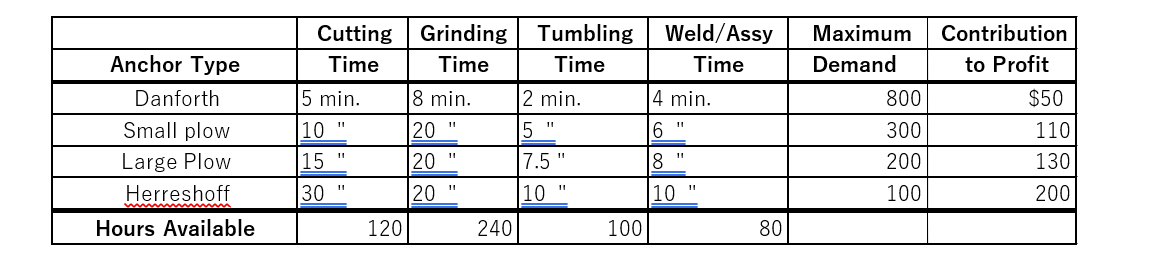
Each anchor requires metal to be cut, ground, tumbled and finally welded and assembled. Because of earlier foresight, Ed has stockpiled plenty of raw material in the form of steel bars, sheets, and tubes. The production data for each anchor of each type in the next cycle is as follows:Ed needs to know how many of each type of anchor he should plan to produce in order to maximize his contribution to profit. We will define D, SP, LP and H to be the number of Danforths, small plows, large plows and Herreshoffs that Ed decides to produce. Converting all the production times to minutes, the complete formulation will be as follows:

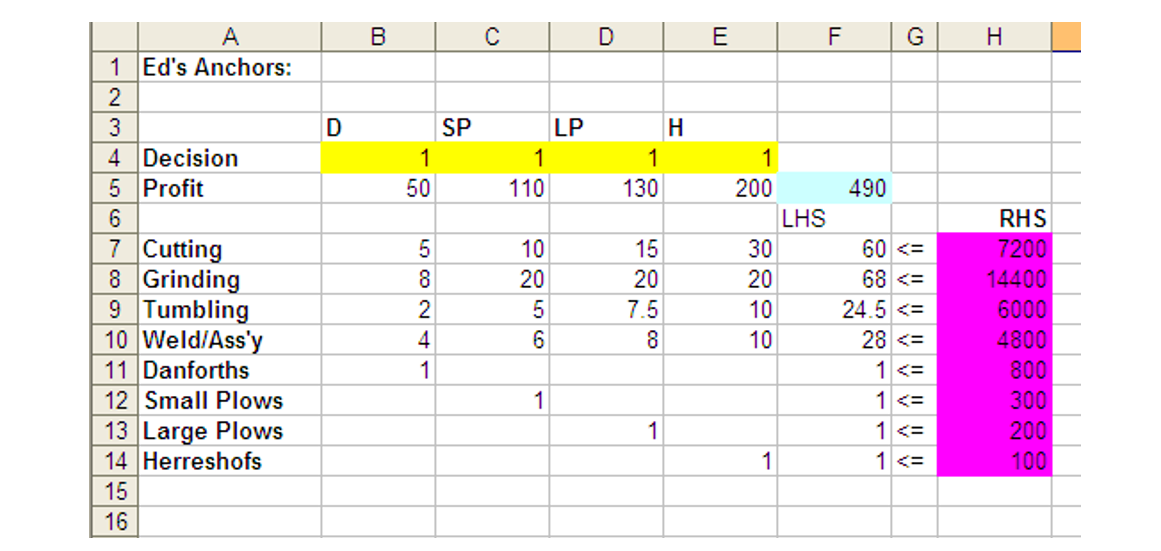
We can enter this formulation into Excel using trial values for the decisions, the number of anchors of each type to be produced. (Using a trial value of 1 lets you quickly ensure that your formulas are correct; that is, that the value of the left hand side, or LHS, of each inequality is correct.) The constraint limits, or Right Hand Sides (RHS) are entered as numbers. The model is shown below.

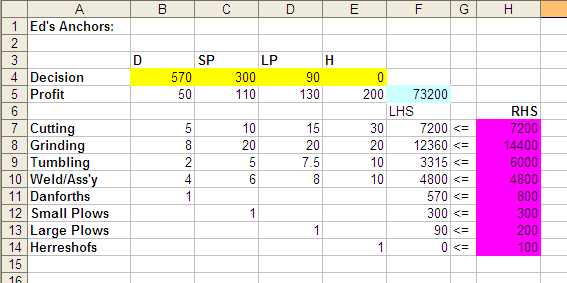
After calling up the Solver and solving the problem the sheet appears:

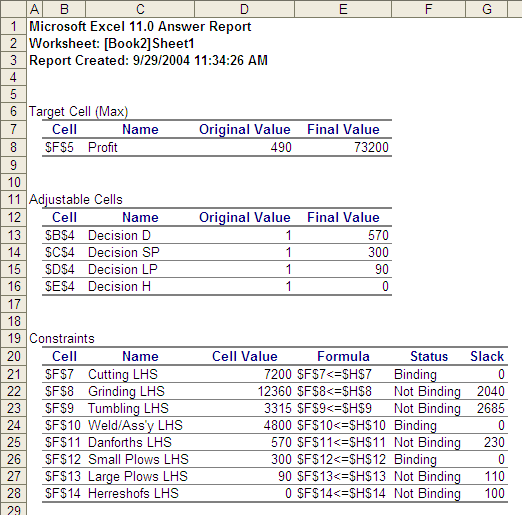
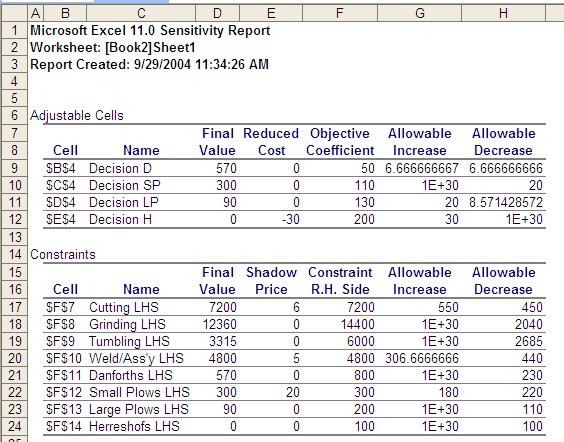
The answer and sensitivity reports below are all you need to answer the questions that follow (there is no need to enter this problem into excel):

a) Ed notices that your plan does not call for any Hereshoffs to be produced. He then says that he has promised 2 of these to special customers. Using the sensitivity report output above, what can you tell Ed about the cost of his promise? (3 marks)

b) The strong demand for Danforths has led Ed to think of raising the price, which would result in a $6 increase per anchor in contribution. Ed has evidence that such a small increase in price will not affect the demand for Danforths. What will be the effect on the optimal solution of such a change? (Note: Dont re-solve the problem. Use your output from a) to indicate what you can say about Eds change in price.) (3 marks)

c) Ed has the chance to hire some part-time welding support from another business, but it is expensive. The "standard" welding hour charge which he used to compute the contribution margins was $25/hr, but he will have to pay $85/hr to buy additional welding support. How many hours should Ed buy at this price? (Note that the units of measurement in the solution are minutes that must be converted to hours to complete this part of the question.) (3 marks)

Cutting Time Grinding Time Tumbling Time Weld/Assy Time 4 min. 15 min. 8 min. 2 min. Maximum Demand 800 300 200 100 Contribution to Profit $50 110 130 200 11 Anchor Type Danforth Small plow Large Plow Herreshoff Hours Available 5 6 10" 15 30 20 20 20 7.5" 8 10 " 10 120 240 100 80 0 B C D E F G H D SP LP H 1 50 1 110 130 490 . 1 Ed's Anchors: 2 3 4 Decision 5 Profit 6 7 Cutting 8 Grinding 9 Tumbling 10 Weld/Ass'y 11 Danforths 12 Small Plows 13 Large Plows 14 Herreshofs 15 16 5 8 2 4 1 10 20 5 6 15 20 7.5 8 1 200 LHS 30 20 10 10 60