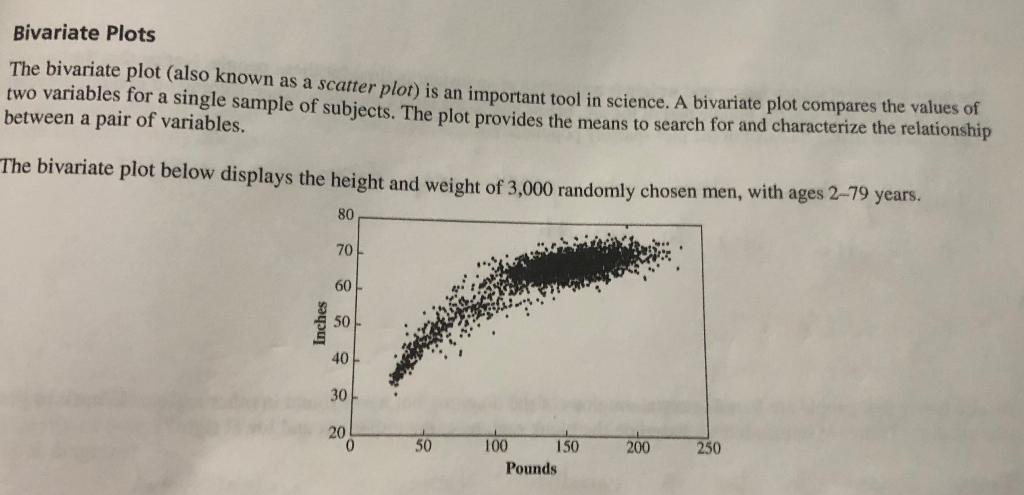
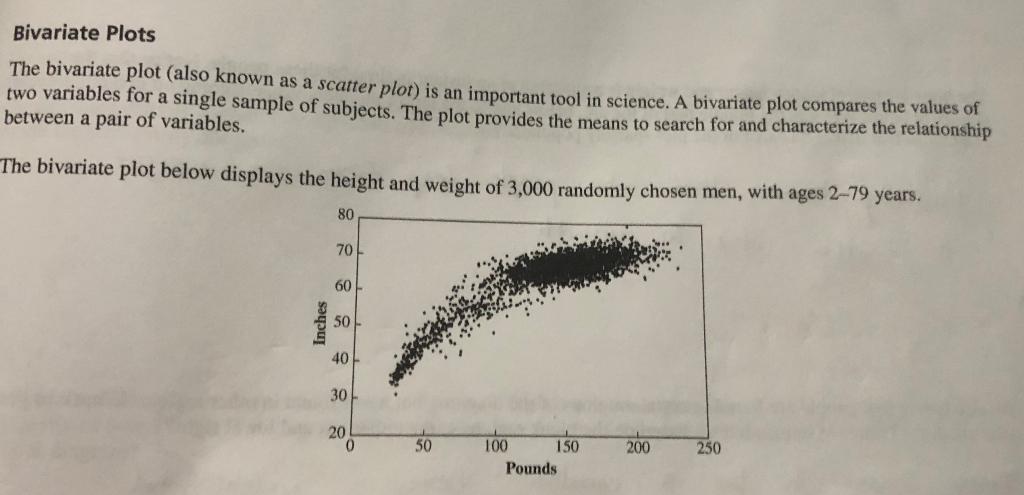
estion:

Calculate the weighted average cost of capital (WACC) for PDI.

E/V80.00%

Cost of equity9.40%

Risk-free rate 3.00%

Beta 1.28

Market equity risk premium 5.00%

D/V20.00%

Cost of debt4.00%

Corporate tax rate40.00%

WACC 80% x 9.40%) + [20% x 4% x (1 - 40%)]= 8.00% WACC = (E/V x Re) + ((D/V x Rd) x (1 - T))

*Cost of equityRisk free rate of return + (Beta * Risk premium) = 3% + (1.28 x 5%) 0.094

Givend the above, I cannot get the following:

Sum of FCF PV =?

Terminal value =?

Present value of terminal value =?

Total value of PDI =?

Assumptions

Discount rate ?

Terminal value ?

O + 9 iii. A second point charge +q is placed to the right of the Gaussian surface as shown. 1. Is the value of 1 greater than, less than, or equal to the value of P in part iii? Explain. 2. Is the value of the flux through the entire Gaussian surface greater than, less than, or equal to the value of the flux through the entire Gaussian surface in part iii? Explain. (Hint: Recall Gauss's Law.)(17) 1. Consider a random experiment that consists of throwing a dart at a triangle-shaped target with vertices at the (x, y) positions (-1, -1), (2, -1), and (-1, 2), resulting in outcome (x, y), the point where the dart hits. Assume that the dart always hits the target and that the probability distribution is uniform over the surface of the target. That is, the bivariate probability density function (pdf), fxY(x, y), has constant value C over the triangle and value 0 outside the triangle. Let the corresponding bivariate cumulative distribution function (CDF) be Fxv(x, y). a. Sketch a bird's-eye view, looking straight down from above, showing the borders and "footprint" of pdf fxY(x, y) on the x-y plane. b. Find the numeric value of pdf fxY(x, y) for x = 0, y = 0. Explain your work. c. Find the numeric value of CDF Fxy(x, y) for x = 0, y = 0. Explain your work.Bivariate Plots The bivariate plot (also known as a scatter plot) is an important tool in science. A bivariate plot compares the values of two variables for a single sample of subjects. The plot provides the means to search for and characterize the relationship between a pair of variables. The bivariate plot below displays the height and weight of 3,000 randomly chosen men, with ages 2-79 years. 80 70 60 Inches 50 40 30 20 0 50 100 150 200 250 Pounds