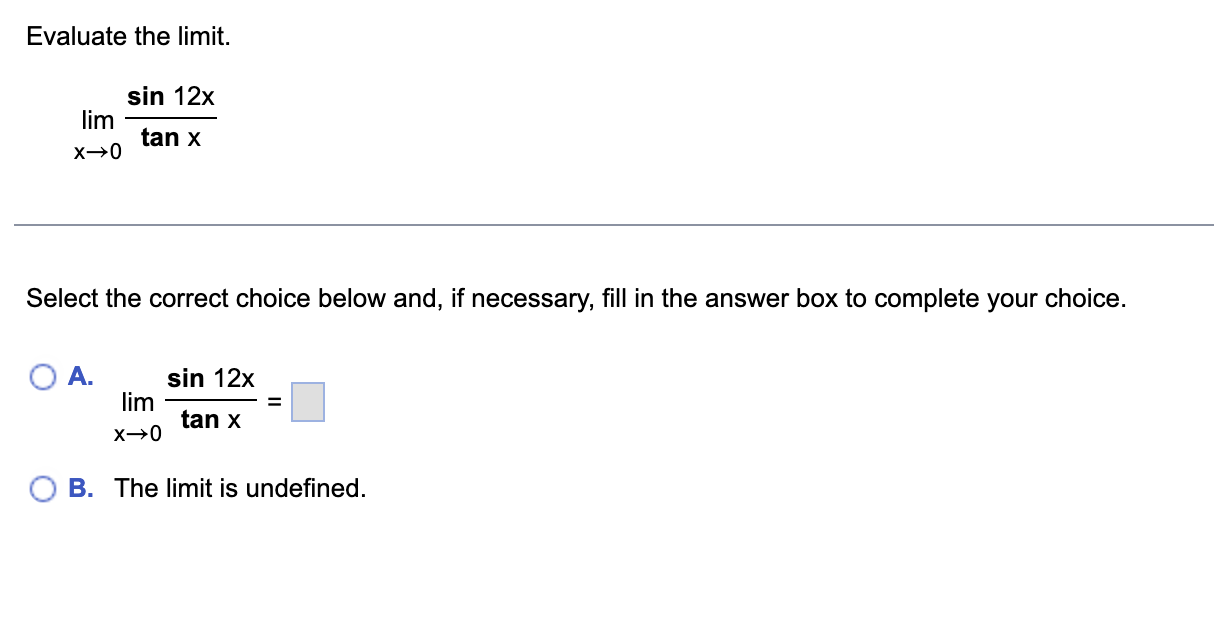
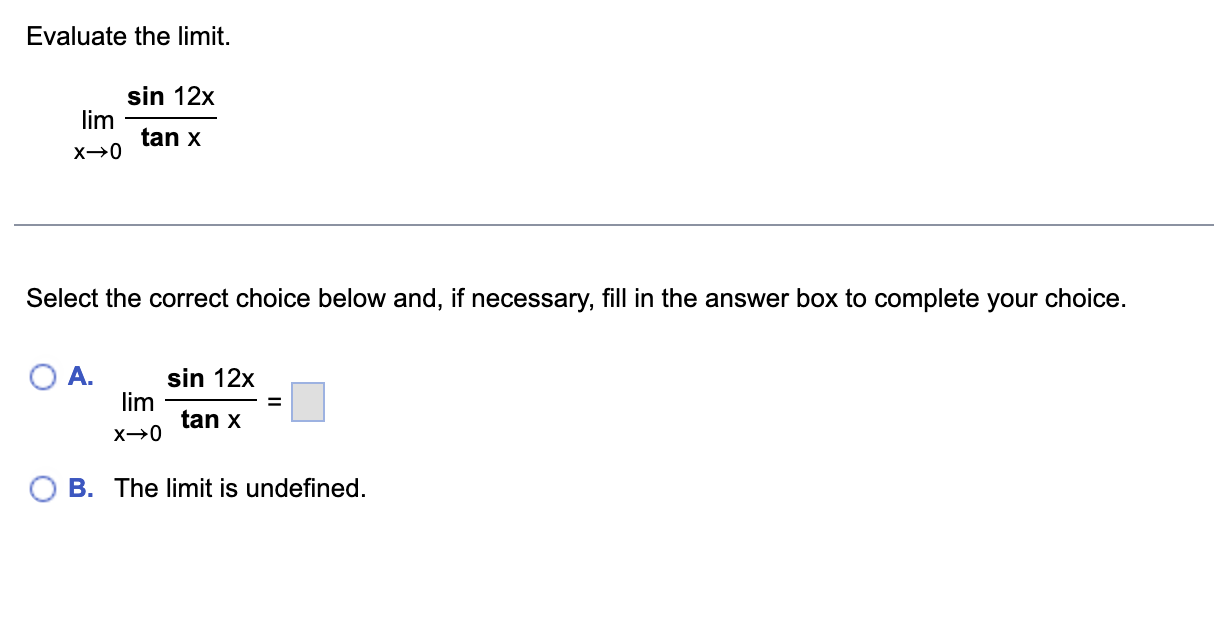
Question: Evaluate the limit. sin 12x lim X-+ 0 tan x Select the correct choice below and, if necessary, fill in the answer box to complete


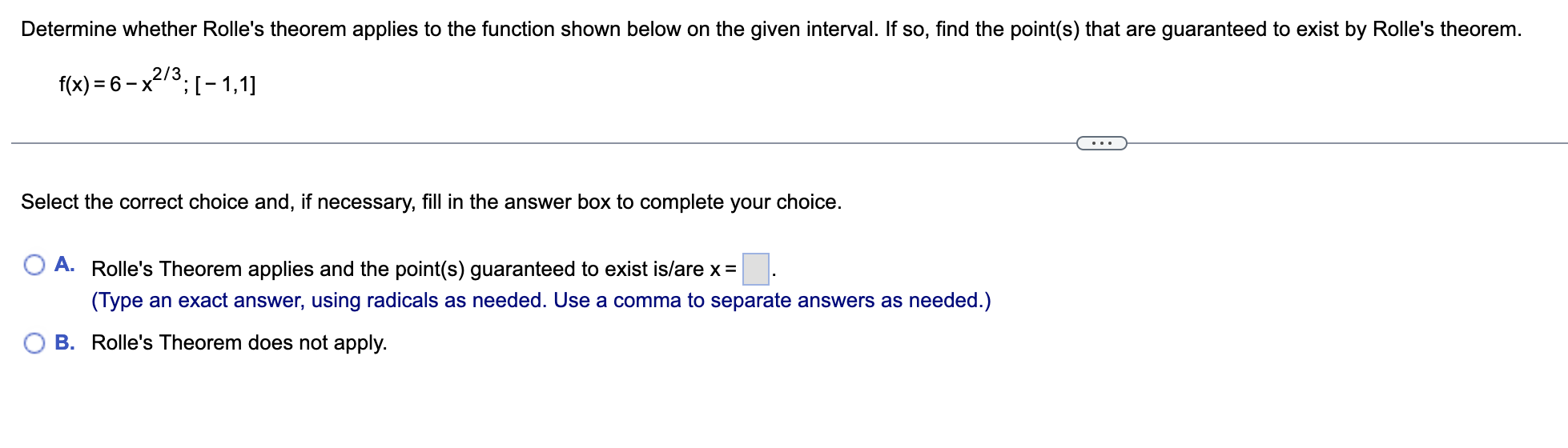






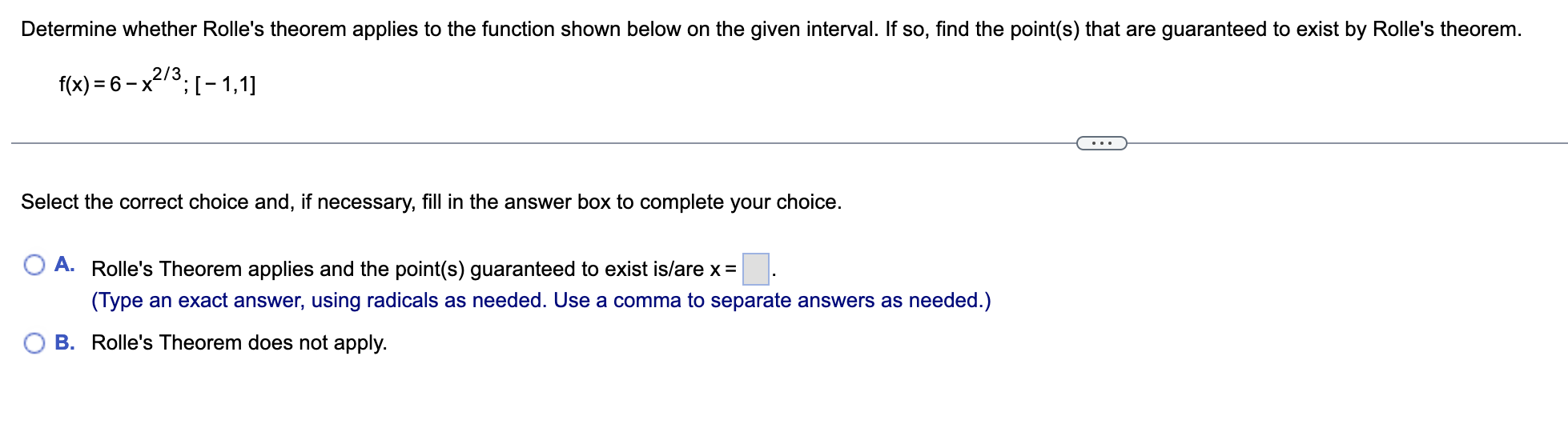




![Rolle's theorem. f(x)=6x2/3;[-1,1] Select the correct choice and, if necessary, ll in](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66799965e2832_15766799965ac8aa.jpg)
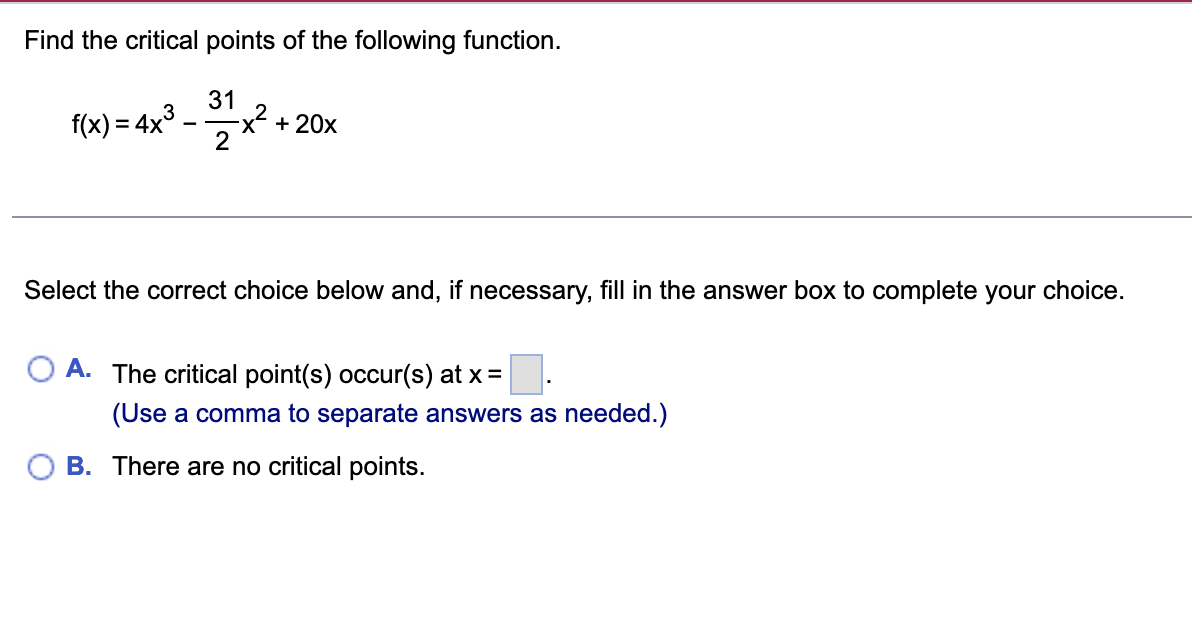
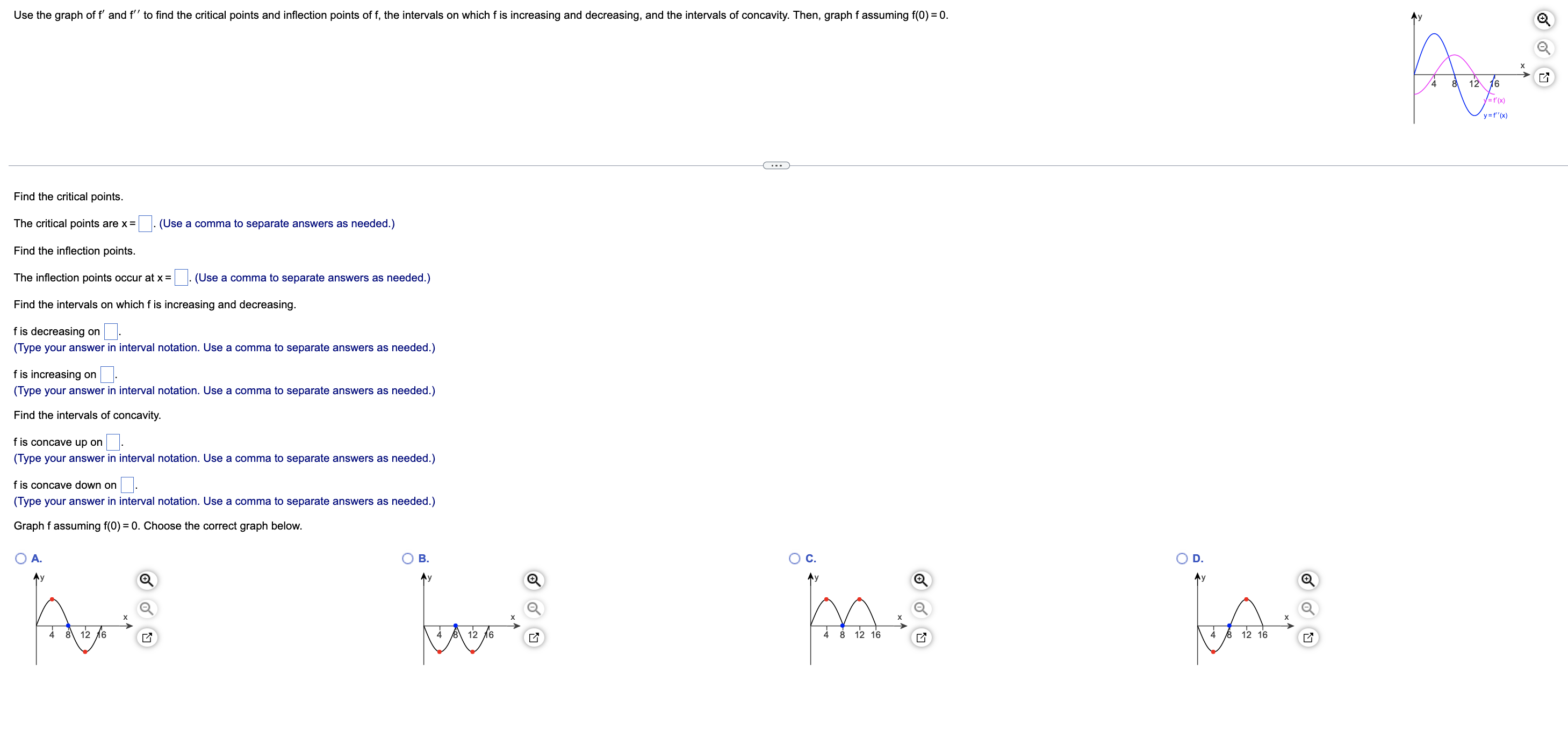
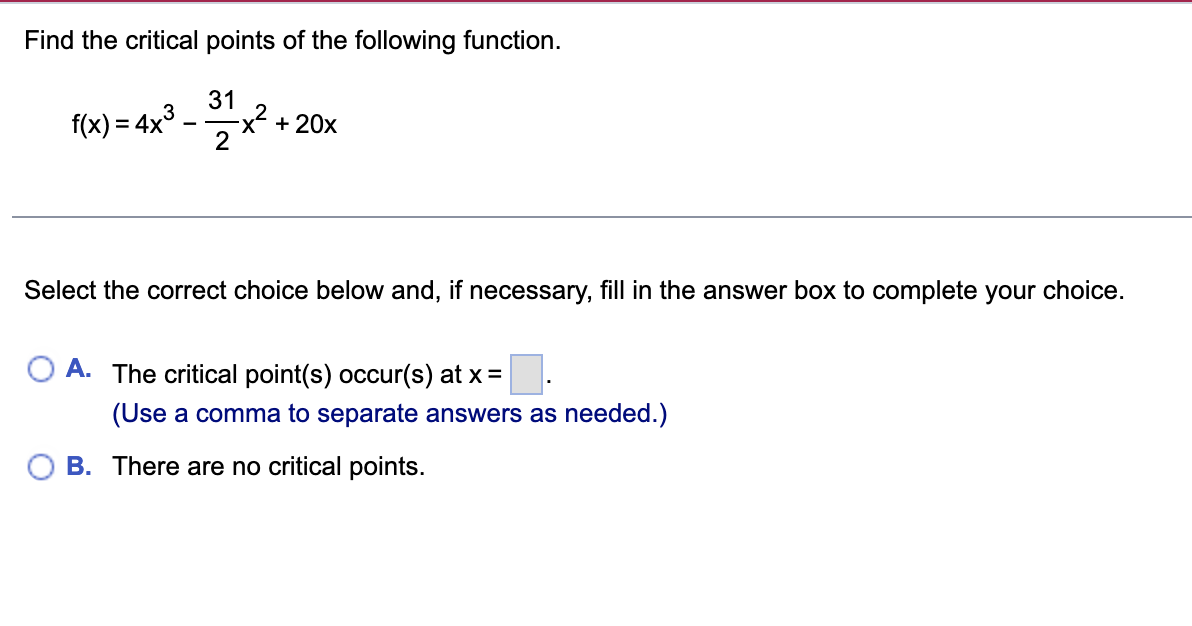
Evaluate the limit. sin 12x lim X-+ 0 tan x Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. sin 12x lim X - 0 tan x O B. The limit is undefined.A 6-foot-tall woman walks at 8 ftls toward a street light that is 24 ft above the ground. What is the rate of change of the length of her shadow when she is 18 ft from the street light? At what rate is the tip of her shadow moving? Let L be the length of the woman's shadow and let x be the woman's distance from the street light. Write an equation that relates L and x. Differentiate both sides of the equation with respect to t' dL dx dt ' ( dt The rate of change of the length of the woman's shadow is V when she is 18 ft from the street light. (Type an exact answer in simplied form) The tip of her shadow moves at a rate of V when she is 18 ft from the street light, (Type an exact answer in simplied form.) dy Use implicit differentiation to find dx exy = 2y dy dxDetermine whether Rolle's theorem applies to the function shown below on the given interval. If so. find the point(s) that are guaranteed to exist by Rolle's theorem. f(x)=6x2/3;[-1,1] Select the correct choice and, if necessary, ll in the answer box to complete your choice. '33? A- Rolle's Theorem applies and the point(s) guaranteed to exist islare x = (Type an exact answer, using radicals as needed. Use a comma to separate answers as needed.) {:3 B. Rolle's Theorem does not apply. Find the derivative of the following function. y = e"* sin x dy dxAn object thrown vertically upward from the surface of a celestial body at a velocity of 35 m/s reaches a height of s = - 0.7t2 + 35t meters in t seconds. a. Determine the velocity v of the object after t seconds. b. When does the object reach its highest point? c. What is the height of the object at the highest point? d. When does the object strike the ground? e. With what velocity does the object strike the ground? f. On what intervals is the speed increasing? . . . a. The object's velocity after t seconds is v(t) = b. It takes the object to reach its highest point. (Simplify your answer.) c. The object reaches a maximum height of (Simplify your answer.) d. The object strikes the ground after (Simplify your answer.) e. The object strikes the ground with the velocity (Simplify your answer.) f. The speed is increasing on the interval(s). (Simplify your answer. Type your answer in interval notation. Use a comma to separate answers as needed.)Find the critical points of the following function. 31 f(x) = 4x3 - ?x2 + 20x Select the correct choice below and, if necessary, ll in the answer box to complete your choice. '33:? A- The critical point(s) occur(s) at X: (Use a comma to separate answers as needed.) {:1- B. There are no critical points. Use the graph of f' and f" to find the critical points and inflection points of f, the intervals on which f is increasing and decreasing, and the intervals of concavity. Then, graph f assuming f(0) = 0. 12 16 =(x ) y= 1"' ( x ) C.. Find the critical points. The critical points are x = ]. (Use a comma to separate answers as needed.) Find the inflection points. The inflection points occur at x = . (Use a comma to separate answers as needed.) Find the intervals on which f is increasing and decreasing. f is decreasing on. Type your answer in interval notation. Use a comma to separate answers as needed.) f is increasing on. "Type your answer in interval notation. Use a comma to separate answers as needed.) Find the intervals of concavity. f is concave up on. (Type your answer in interval notation. Use a comma to separate answers as needed.) f is concave down on. (Type your answer in interval notation. Use a comma to separate answers as needed.) Graph f assuming f(0) = 0. Choose the correct graph below. O A. O B. O c. O D. AV Ay Ay 8 12 16 1 8 12 16 X 12 3 12 16
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


