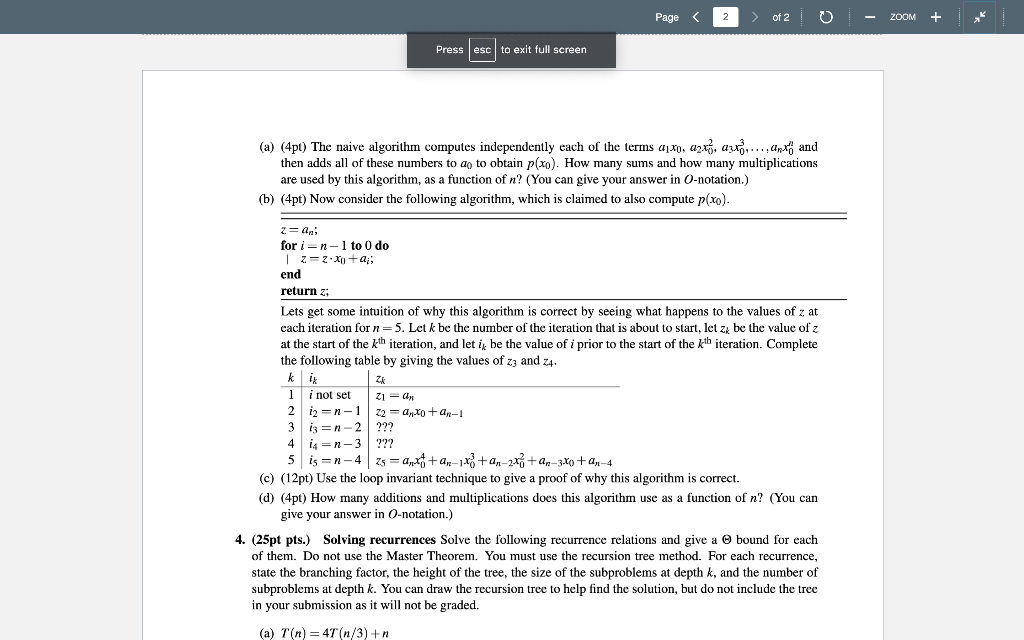
Evaluating Polynomials Consider a polynomial given by p(x) = a0 + a1x + a2x2 + + anxn. Consider the problem of evaluating it at some point x0, i.e. computing p(x0). CMPSC 465, Spring 2023, HW 2 1 (a) (4pt) The naive algorithm computes independently each of the terms a1x0, a2x20, a3x30,...,anxn0 and then adds all of these numbers to a0 to obtain p(x0). How many sums and how many multiplications are used by this algorithm, as a function of n? (You can give your answer in O-notation.) (b) (4pt) Now consider the following algorithm, which is claimed to also compute p(x0). z = an; for i = n 1 to 0 doz = z x0 +ai; end return z; Lets get some intuition of why this algorithm is correct by seeing what happens to the values of z at each iteration for n = 5. Let k be the number of the iteration that is about to start, let zk be the value of z at the start of the kth iteration, and let ik be the value of i prior to the start of the kth iteration. Complete the following table by giving the values of z3 and z4. k ik zk 1 i not set z1 = an 2 i2 = n 1 z2 = anx0 +an1 3 i3 = n 2 ??? 4 i4 = n 3 ??? 5 i5 = n 4 z5 = anx40 +an1x30 +an2x20 +an3x0 +an4 (c) (12pt) Use the loop invariant technique to give a proof of why this algorithm is correct. (d) (4pt) How many additions and multiplications does this algorithm use as a function of n? (You can give your answer in O-notation.)

3. (24 pts.) Evaluating Polynomials Consider a polynomial given by p(x)=a0+a1x+a2x2++anxn. Consider the problem of evaluating it at some point x0, i.e. computing p(x0). CMPSC 465, Spring 2023, HW 2 1 (a) (4pt) The naive algorithm computes independently each of the terms a1x0,a2x02,a3x03,,anx0n and then adds all of these numbers to a0 to obtain p(x0). How many sums and how many multiplications are used by this algorithm, as a function of n ? (You can give your answer in O-notation.) (b) (4pt) Now consider the following algorithm, which is claimed to also compute p(x0). z=an; for i=n1 to 0 do z=zx0+ai; end return z; Lets get some intuition of why this algorithm is correct by seeing what happens to the values of z at each iteration for n=5. Let k be the number of the iteration that is about to start, let zk be the value of z at the start of the kth iteration, and let ik be the value of i prior to the start of the kth iteration. Complete the following table by giving the values of z3 and z4. (a) (4pt) The naive algorithm computes independently each of the terms a1x0,a2x02,a3x03,,anx0n and then adds all of these numbers to a0 to obtain p(x0). How many sums and how many multiplications are used by this algorithm, as a function of n ? (You can give your answer in O-notation.) (b) (4pt) Now consider the following algorithm, which is claimed to also compute p(x0). z=an; for i=n1 to 0 do 1z=zx0+ai; end return z; Lets get some intuition of why this algorithm is correct by seeing what happens to the values of z at each iteration for n=5. Let k be the number of the iteration that is about to start, let zk be the value of z at the start of the kth iteration, and let ik be the value of i prior to the start of the kth iteration. Complete the following table by giving the values of z3 and z4. \begin{tabular}{l|l|l} k & ik & zk \\ \hline 1 & i not set & z1=an \\ 2 & i2=n1 & z2=anx0+an1 \\ 3 & i3=n2 & ??? \\ 4 & i4=n3 & ??? \\ 5 & i5=n4 & z5=anx04+an1x03+an2x02+an3x0+an4 \end{tabular} (c) (12pt) Use the loop invariant technique to give a proof of why this algorithm is correct. (d) (4pt) How many additions and multiplications does this algorithm use as a function of n ? (You can give your answer in O-notation.) 4. (25pt pts.) Solving recurrences Solve the following recurrence relations and give a bound for each of them. Do not use the Master Theorem. You must use the recursion tree method. For each recurrence, state the branching factor, the height of the tree, the size of the subproblems at depth k, and the number of subproblems at depth k. You can draw the recursion tree to help find the solution, but do not include the tree in your submission as it will not be graded. (a) T(n)=4T(n/3)+n