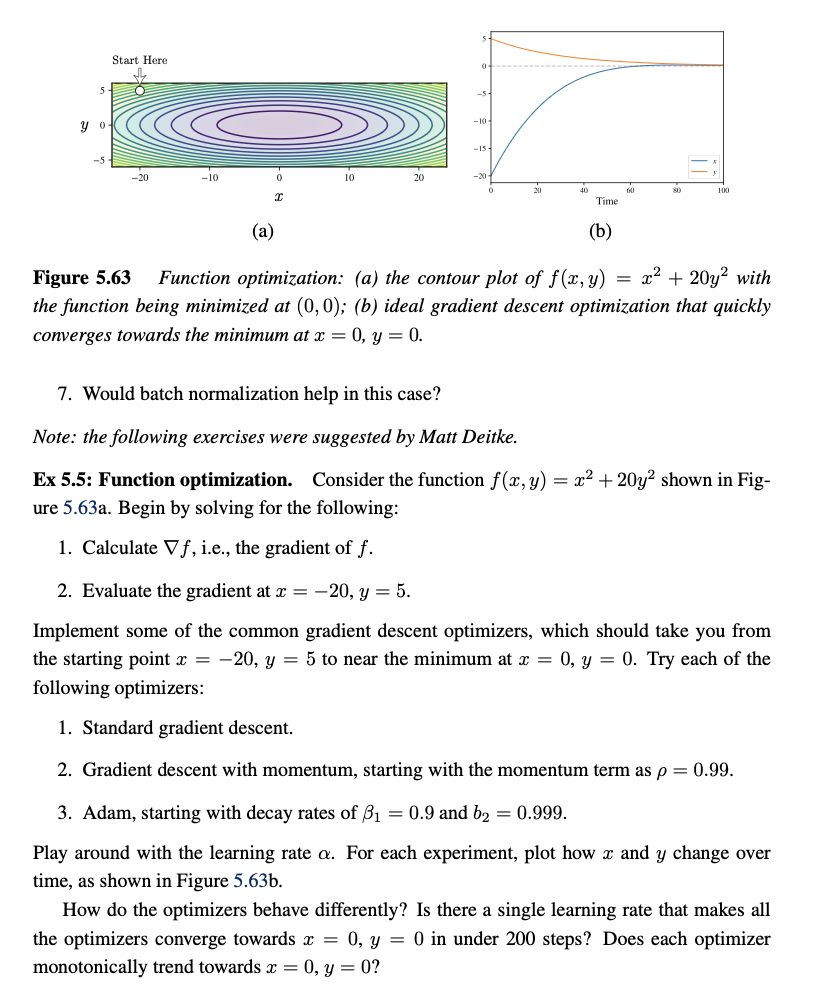
Ex $5\mathrm{.}5$: Function optimization. Consider the function $f(x,y)=x^2+20y^2$ shown in Fig$-$

ure $5\mathrm{.}63$a$.$ Begin by solving for the following:

Calculate gradf, i$.$e$.,$ the gradient of $f.$

Evaluate the gradient at $x=-20,y=5.$

Implement some of the common gradient descent optimizers, which should take you from

the starting point $x=-20,y=5$ to near the minimum at $x=0,y=0.$ Try each of the

following optimizers:

Standard gradient descent.

Gradient descent with momentum, starting with the momentum term as $=0\mathrm{.}99.$

Adam, starting with decay rates of ${}_1=0\mathrm{.}9$ and $b_2=0\mathrm{.}999.$

Play around with the learning rate $.$ For each experiment, plot how $x$ and $y$ change over

time, as shown in Figure $5\mathrm{.}63$b$.$

How do the optimizers behave differently? Is there a single learning rate that makes all

the optimizers converge towards $x=0,y=0$ in under $200$ steps? Does each optimizer

monotonically trend towards $x=0,y=0?$Figure $5\mathrm{.}63$ Function optimization: $($a$)$ the contour plot of $f(x,y)=x^2+20y^2$ with

the function being minimized at $(0,0)$;$(b)$ ideal gradient descent optimization that quickly

converges towards the minimum at $x=0,y=0.$

Would batch normalization help in this case?

Note: the following exercises were suggested by Matt Deitke.

Ex $5\mathrm{.}5$: Function optimization. Consider the function $f(x,y)=x^2+20y^2$ shown in Fig$-$

ure $5\mathrm{.}63$a$.$ Begin by solving for the following:

Calculate gradf, i$.$e$.,$ the gradient of $f.$

Evaluate the gradient at $x=-20,y=5.$

Implement some of the common gradient descent optimizers, which should take you from

the starting point $x=-20,y=5$ to near the minimum at $x=0,y=0.$ Try each of the

following optimizers:

Standard gradient descent.

Gradient descent with momentum, starting with the momentum term as $=0\mathrm{.}99.$

Adam, starting with decay rates of ${}_1=0\mathrm{.}9$ and $b_2=0\mathrm{.}999.$

Play around with the learning rate $.$ For each experiment, plot how $x$ and $y$ change over

time, as shown in Figure $5\mathrm{.}63$b$.$

How do the optimizers behave differently? Is there a single learning rate that makes all

the optimizers converge towards $x=0,y=0$ in under $200$ steps? Does each optimizer

monotonically trend towards $x=0,y=0?$