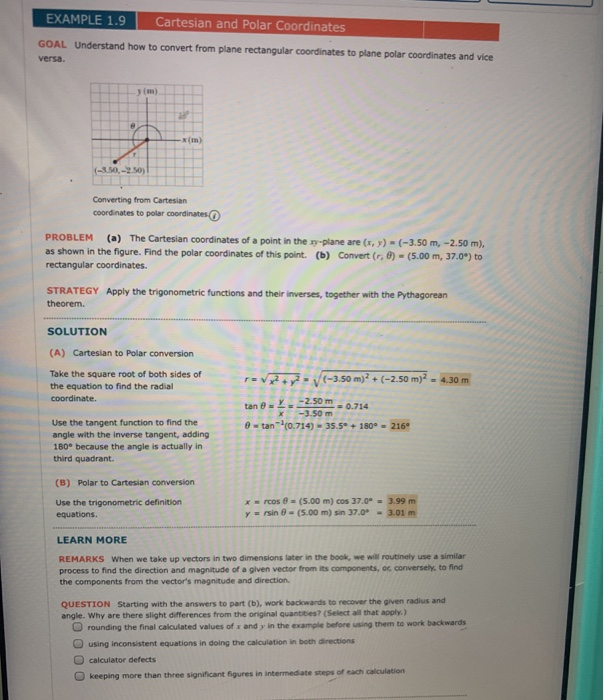
EXAMPLE 1.9 Cartesian and Polar Coordinates GOAL Understand how to convert from plane rectangular coordinates to plane polar coordinates and vice versa. y (m). (-3.50,-2.50) 28 x(m) Converting from Cartesian coordinates to polar coordinates SOLUTION PROBLEM (a) The Cartesian coordinates of a point in the xy-plane are (x, y) = (-3.50 m, -2.50 m), as shown in the figure. Find the polar coordinates of this point. (b) Convert (r, 8) - (5.00 m, 37.0) to rectangular coordinates. STRATEGY Apply the trigonometric functions and their inverses, together with the Pythagorean theorem. (A) Cartesian to Polar conversion Take the square root of both sides of the equation to find the radial coordinate. Use the tangent function to find the angle with the inverse tangent, adding 180 because the angle is actually in third quadrant. (B) Polar to Cartesian conversion Use the trigonometric definition equations. r=+(-3.50 m)2 + (-2.50 m)2 = 4.30 m -2.50 m -3.50 m etan (0.714)- 35.5+ 180-216 tan 8== X = 0.714 x=rcos 8= (5.00 m) cos 37.0 = 3.99 m y = rsin 8- (5.00 m) sin 37.0 - 3.01 m LEARN MORE REMARKS When we take up vectors in two dimensions later in the book, we will routinely use a similar process to find the direction and magnitude of a given vector from its components, or, conversely, to find the components from the vector's magnitude and direction. QUESTION Starting with the answers to part (b), work backwards to recover the given radius and angle. Why are there slight differences from the original quantities? (Select all that apply.) Orounding the final calculated values of x and y in the example before using them to work backwards using inconsistent equations in doing the calculation in both directions O calculator defects Okeeping more than three significant figures in intermediate steps of each calculation take up vectors in two dimensions later in the book, we will routinely use a similar process to find the direction and magnitude of a given vector from its components, or, conversely, to find the components from the vector's magnitude and direction. QUESTION Starting with the answers to part (b), work backwards to recover the given radius and angle. Why are there slight differences from the original quantities? (Select all that apply.) O rounding the final calculated values of x and y in the example before using them to work backwards using inconsistent equations in doing the calculation in both directions calculator defects keeping more than three significant figures in intermediate steps of each calculation PRACTICE IT Use the worked example above to help you solve this problem. (a) The Cartesian coordinates of a point in the xy-plane are (x, y) = (-3.27, -2.42) m. Find the polar coordinates of this point. r= m 0- 8- yw (b) Convert (r, 0) (4.63 m, 35.4) to rectangular coordinates. = x= m EXERCISE (a) Find the polar coordinates corresponding to (x, y) = (3.34, 1.69) m. m Need Help? 0 0 m (b) Find the Cartesian coordinates corresponding to (r, 0) (3.95 m, 52.1). m m HINTS: GETTING STARTED Read It I'M STUCK!