Example DTM:
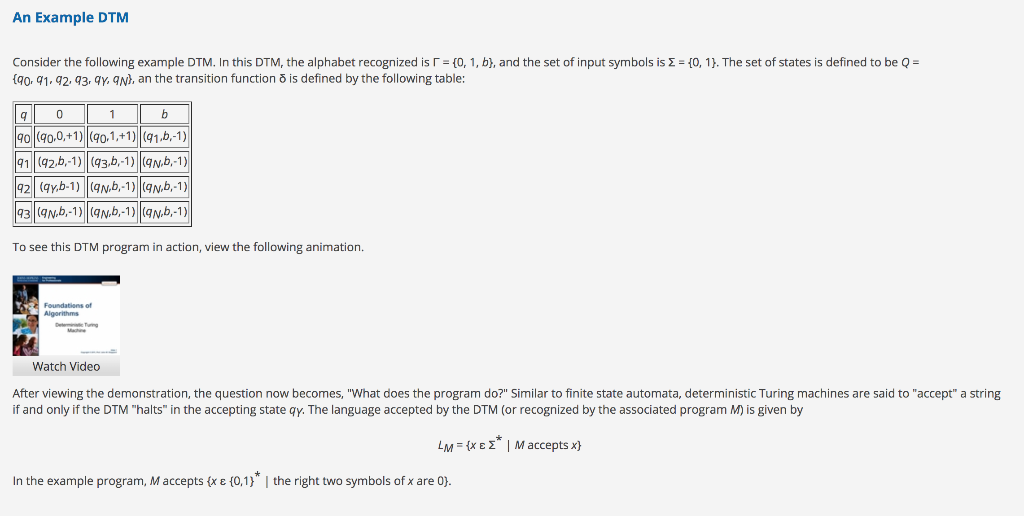
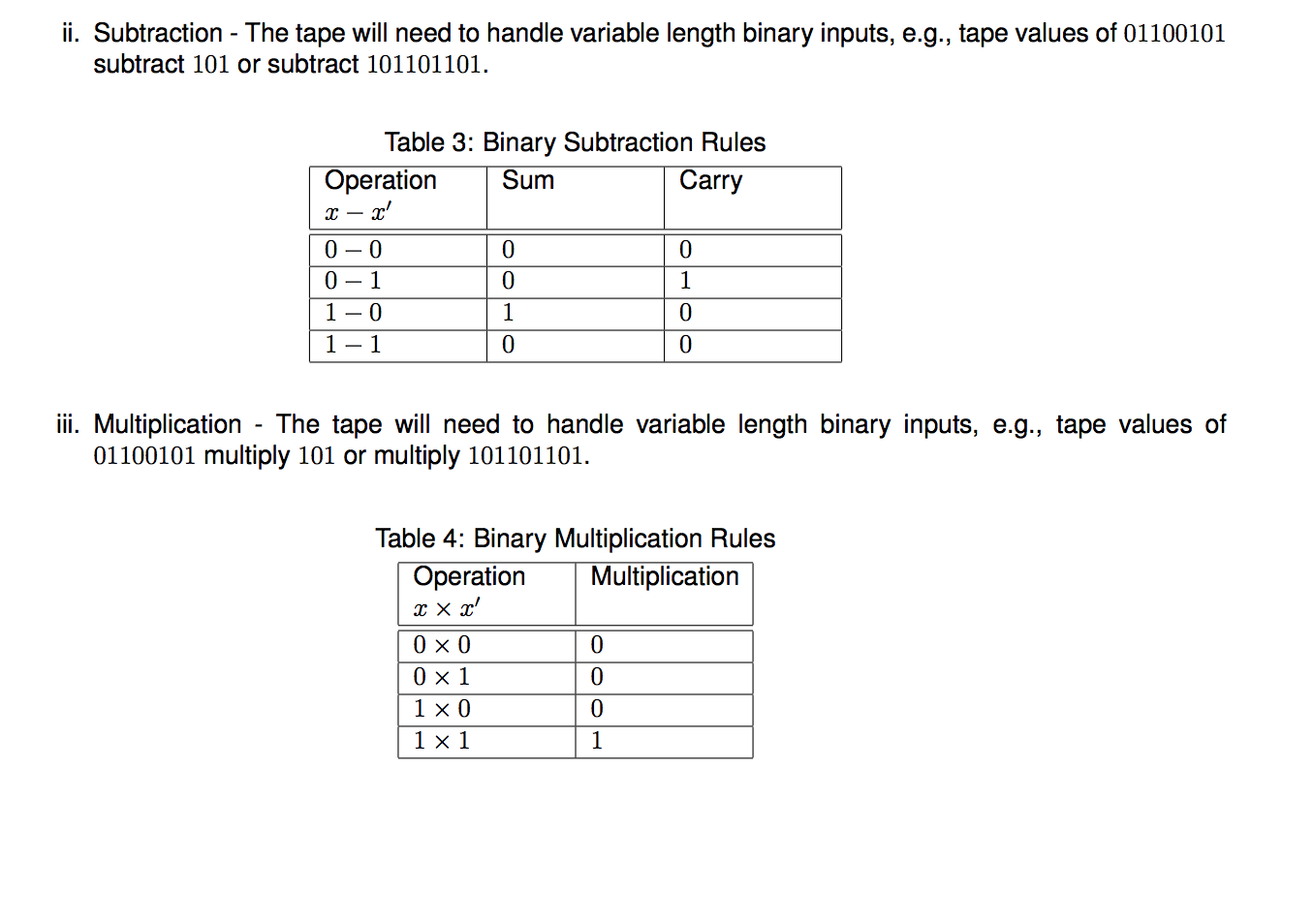
2. [50 Points] Deterministic Turing Machine (DTM) In 1900, mathematician David Hilbert enumerated 23 mathematical problems he considered challenges for the coming century. The tenth problem is his list concerned algorithms: Given a polynomial, find an "algorithm" for determining whether the polynomial has an integral root. In the way Hilbert phrased the above problem, he explicitly asked that an algorithm be "devised". As we now know, no algorithm exists for this task if the poly- nomial is de-fined on several variables. That is, the above problem is algorithmically unsolvable. However, mathematicians of that period could not come to this conclusion with their intuitive notion of algorithm. Although our intuitive notion of an algorithm is enough to "devise" solutions for certain problems (the ones a computer can solve), it is useless for showing that no algorithm exists for a particular task, as our intuitive notion is not a formal one. So, proving that an algorithm does not exist required having a clear definition of algorithm. Such a definition was simultaneously given in 1936 by Alonzo Church and Alan Turing.Church used a notational system called the lamda calculus to precisely define algorithms. Turing did it with his "machines" This connection between the informal notion of algorithm and the precise definition is known as the the Church-Turing thesis. More precisely, Turing proposed to adopt the Turing machine that halts on all inputs as the precise formal notion corresponding to our intuitive notion of an "algorithm. Note that the Church-Turing thesis is not a theorem, but a "thesis, as it asserts that a certain informal concept (algorithm) corresponds to a certain mathematical object (Turing machine). Since Turing machines can only deal with decision problems, you may find very strange the fact that a Turing machine is a formal counterpart of our intuitive notion of an algorithm, as many computational problems are not decision problems. Well, keep in mind that every computational problem is either equivalent to a decision problem or is at least as "hard" as some decision problem. So, the restriction to decision problems is not a problem. Besides helping us understand what we can or cannot do with computers, Turing machines can also be used to formally define the complexity of an algorithm. In this problem you will implement two variants of a DTM. The definition and example are provided below followed by the two required implementations. A deterministic Turing machine consists of the following: In this problem you will implement two variants of a DTM. The definition and example are provided below followed by the two required implementations. A deterministic Turing machine consists of the following: A finite state control, A tape consisting of a two-way sequence of tape squares, and A read-write head. A given DTM is manipulated through the execution of a program utilizing the following components: A finite set I of symbols, A finite set Q of states (qo is designated as the start state and qy and qn are designated as halting states), where {90,9h} E Q, The direction. s = (left, right, halt), where left = -1 and right = +1, in which to move the tape head s EQ A transition function 8: (Q-{qy, qn}) x I Qx{+1,0, -1}, Scras a set of input symbols, and be (T-) corresponds to the "blank symbol" (#) This allows a DTM to be represented as a finite set of program lines with the form of a 6-tuple TM M = (T,Q,,8,,b). In other words, the DTM will scan the tape, and the transition function will read the symbol from I currently written on the table and determine what character to write in its place as well as which direction s to move the read-write head. Presumably, if the program indicates +1, the head moves to the right, if the program indicates -1, the head moves to the left and if the program indicates O, the head stays still. To see how a DTM works, suppose we have cl as a set of input symbols and be (T-) a "blank symbol" (#). Next suppose we have an input string x * where we place the symbols of u in consecutive cells of the tape in positions 1... X. All other cells on the tape are assumed to have b. The program will begin in state go with the read-write head scanning square 1 and proceed according to the transition function. If the current state of the DTM is ever qy or qn, then the program terminates. On the other hand, if the current state is in Q - {qy, qn}, then the program continues. When transitioning, the read-write head will first erase the symbol in the square it is examining and then write the new symbol as specified by the transition function. The read-write head then either moves one position to the right or one position to the left, and the Finite State Control updates the state to some successor q'. Because we have limited the set of halting (or terminal) states to qy qn, we note that a DTM is only able to solve problems that return a Boolean result. In particular, we say that a DMT is used to solve decision problems where qy indicates the DMT has decided yes and an indicates the DTM has decided no. The set of states is defined to be Q = 90, 91, 42, 43, qy, qn, and the transition function 8 is defined by the following table: 0, 1, [R] 0,!b, [L] b, [L] 0,!b, [L] start -0 start - 90 6,14_ 91 _ 92 0, 10, 14 mm qy b, [L] 1, !b, [L] b, [L] 1!b, [L] 0, 1, b, [L] Figure 1: DTM State Diagram 1b Table 1: DTM model illustrated in Figure 1. Q-{qy, qn} 0 90 (90, 0, +1) (90,1, +1) (91,6, -1) (42,6, -1) (93,6, -1) (qn,b, -1) 92 (qy, b, -1) (qn,b, -1) (an, b, -1) (qn,b, -1) (qn,b, -1) (qn,b, -1) To reiterate how the DTM works, Table 1 represents the states q = Q - {qy, qn}, symbols in z, and the direction the read-write head moves (s). Starting with the initial state represented with co the finite controller reads the initial symbol represented by c. At each step the controller reads the symbol x on the tape at state q, enters the state q' = Q = 40,91, 92, 93, 94, 9N, writes the symbol x' in the current cell, erasing, and moves in the direction identified by s. This is represented as the five-tuple (q,x, d', x', 8) TM. For Table 1 the DTM is represented by the following finite-state machine in Figure 1. The edges in Figure 1 are labeled with the sym- bol(s) on the tape, a symbol that overwrites the current symbol (if any), and the direction of tape movement. For example, (1, !b, [R]) on the edge between 91 and 93 denotes when the read/write head is over a symbol 1 while in state qi overwrite the 1 with b and move the tape to the right. Please note that you can define other symbols in T and you should. Consider representing two unary numbers on the tape and performing the operations in your assignment. If you include S, E in your set I you could use those symbols to recognize the start of data on the tape (S) and the end of data on the tape (E) making those symbols available to you in your state modeling. Remember that each state must fully define the operation of the DTM in that state for each symbol in I. Please note that you can define other symbols in I and you should. Consider representing two unary numbers on the tape and performing the operations in your assignment. If you include S, E in your set I you could use those symbols to recognize the start of data on the tape (S) and the end of data on the tape (E) making those symbols available to you in your state modeling. Remember that each state must fully define the operation of the DTM in that state for each symbol in T. (a) [25 Points] Implement the DTM example provided in the Course Content under Module 3. Ensure that your components as listed above are clearly identified in your variable list. The finite-state machine with the individual states, state table and five-tuple TM are shown in the above example. You should implement the following methods: i. States method, this method should have all of the operations of your TM. ii. Program line that executes the operations for each identified state, this should follow the n-tuple TM as described above for M. iii. Print method that outputs the change in tape (2 30 write the outputs to a file (b) (25 Points] Expand the implementation of the DTM in part (a) to perform additional binary operations (addition, subtraction, multiplication) at each state. You should implement the following methods that will allow for other operations: i. Addition - The tape will need to handle variable length binary inputs, e.g., tape values of 01100101 add 101 or add 101101101. Table 2: Binary Addition Rules Operation Sum Carry 3+' 0+0 0+1 1+0 1+1 ii. Subtraction - The tape will need to handle variable length binary inputs, e.g., tape values of 01100101 subtract 101 or subtract 101101101. ii. Subtraction - The tape will need to handle variable length binary inputs, e.g., tape values of 01100101 subtract 101 or subtract 101101101. Carry Table 3: Binary Subtraction Rules Operation Sum x - x' 0-0 0-1 0 10 1-1 iii. Multiplication - The tape will need to handle variable length binary inputs, e.g., tape values of 01100101 multiply 101 or multiply 101101101. Table 4: Binary Multiplication Rules Operation Multiplication OXO 0 x1 1 x 0 1x1 1 An Example DTM Consider the following example DTM. In this DTM, the alphabet recognized is r = {0, 1, b), and the set of input symbols is 2 = {0, 1). The set of states is defined to be Q = {90,91,92, 93, 94, 9N), an the transition function is defined by the following table: 1 b 90 90(90,0,+1) (90,1,+1) 91,6,-1) 91 (92,6,-1) (93,6,-1) (9.6.-1) 22 (qy.b-1) (99.6.-1) (9.6.-1) 93699.b.-1) (9.6.-1) (9.b.-1) To see this DTM program in action, view the following animation Foundations of Watch Video After viewing the demonstration, the question now becomes, "What does the program do?" Similar to finite state automata, deterministic Turing machines are said to "accept" a string if and only if the DTM "halts" in the accepting state qy. The language accepted by the DTM (or recognized by the associated program M) is given by LM = {xe 2* | M accepts x} In the example program, M accepts (x {0,1}* the right two symbols of x are 0). 2. [50 Points] Deterministic Turing Machine (DTM) In 1900, mathematician David Hilbert enumerated 23 mathematical problems he considered challenges for the coming century. The tenth problem is his list concerned algorithms: Given a polynomial, find an "algorithm" for determining whether the polynomial has an integral root. In the way Hilbert phrased the above problem, he explicitly asked that an algorithm be "devised". As we now know, no algorithm exists for this task if the poly- nomial is de-fined on several variables. That is, the above problem is algorithmically unsolvable. However, mathematicians of that period could not come to this conclusion with their intuitive notion of algorithm. Although our intuitive notion of an algorithm is enough to "devise" solutions for certain problems (the ones a computer can solve), it is useless for showing that no algorithm exists for a particular task, as our intuitive notion is not a formal one. So, proving that an algorithm does not exist required having a clear definition of algorithm. Such a definition was simultaneously given in 1936 by Alonzo Church and Alan Turing.Church used a notational system called the lamda calculus to precisely define algorithms. Turing did it with his "machines" This connection between the informal notion of algorithm and the precise definition is known as the the Church-Turing thesis. More precisely, Turing proposed to adopt the Turing machine that halts on all inputs as the precise formal notion corresponding to our intuitive notion of an "algorithm. Note that the Church-Turing thesis is not a theorem, but a "thesis, as it asserts that a certain informal concept (algorithm) corresponds to a certain mathematical object (Turing machine). Since Turing machines can only deal with decision problems, you may find very strange the fact that a Turing machine is a formal counterpart of our intuitive notion of an algorithm, as many computational problems are not decision problems. Well, keep in mind that every computational problem is either equivalent to a decision problem or is at least as "hard" as some decision problem. So, the restriction to decision problems is not a problem. Besides helping us understand what we can or cannot do with computers, Turing machines can also be used to formally define the complexity of an algorithm. In this problem you will implement two variants of a DTM. The definition and example are provided below followed by the two required implementations. A deterministic Turing machine consists of the following: In this problem you will implement two variants of a DTM. The definition and example are provided below followed by the two required implementations. A deterministic Turing machine consists of the following: A finite state control, A tape consisting of a two-way sequence of tape squares, and A read-write head. A given DTM is manipulated through the execution of a program utilizing the following components: A finite set I of symbols, A finite set Q of states (qo is designated as the start state and qy and qn are designated as halting states), where {90,9h} E Q, The direction. s = (left, right, halt), where left = -1 and right = +1, in which to move the tape head s EQ A transition function 8: (Q-{qy, qn}) x I Qx{+1,0, -1}, Scras a set of input symbols, and be (T-) corresponds to the "blank symbol" (#) This allows a DTM to be represented as a finite set of program lines with the form of a 6-tuple TM M = (T,Q,,8,,b). In other words, the DTM will scan the tape, and the transition function will read the symbol from I currently written on the table and determine what character to write in its place as well as which direction s to move the read-write head. Presumably, if the program indicates +1, the head moves to the right, if the program indicates -1, the head moves to the left and if the program indicates O, the head stays still. To see how a DTM works, suppose we have cl as a set of input symbols and be (T-) a "blank symbol" (#). Next suppose we have an input string x * where we place the symbols of u in consecutive cells of the tape in positions 1... X. All other cells on the tape are assumed to have b. The program will begin in state go with the read-write head scanning square 1 and proceed according to the transition function. If the current state of the DTM is ever qy or qn, then the program terminates. On the other hand, if the current state is in Q - {qy, qn}, then the program continues. When transitioning, the read-write head will first erase the symbol in the square it is examining and then write the new symbol as specified by the transition function. The read-write head then either moves one position to the right or one position to the left, and the Finite State Control updates the state to some successor q'. Because we have limited the set of halting (or terminal) states to qy qn, we note that a DTM is only able to solve problems that return a Boolean result. In particular, we say that a DMT is used to solve decision problems where qy indicates the DMT has decided yes and an indicates the DTM has decided no. The set of states is defined to be Q = 90, 91, 42, 43, qy, qn, and the transition function 8 is defined by the following table: 0, 1, [R] 0,!b, [L] b, [L] 0,!b, [L] start -0 start - 90 6,14_ 91 _ 92 0, 10, 14 mm qy b, [L] 1, !b, [L] b, [L] 1!b, [L] 0, 1, b, [L] Figure 1: DTM State Diagram 1b Table 1: DTM model illustrated in Figure 1. Q-{qy, qn} 0 90 (90, 0, +1) (90,1, +1) (91,6, -1) (42,6, -1) (93,6, -1) (qn,b, -1) 92 (qy, b, -1) (qn,b, -1) (an, b, -1) (qn,b, -1) (qn,b, -1) (qn,b, -1) To reiterate how the DTM works, Table 1 represents the states q = Q - {qy, qn}, symbols in z, and the direction the read-write head moves (s). Starting with the initial state represented with co the finite controller reads the initial symbol represented by c. At each step the controller reads the symbol x on the tape at state q, enters the state q' = Q = 40,91, 92, 93, 94, 9N, writes the symbol x' in the current cell, erasing, and moves in the direction identified by s. This is represented as the five-tuple (q,x, d', x', 8) TM. For Table 1 the DTM is represented by the following finite-state machine in Figure 1. The edges in Figure 1 are labeled with the sym- bol(s) on the tape, a symbol that overwrites the current symbol (if any), and the direction of tape movement. For example, (1, !b, [R]) on the edge between 91 and 93 denotes when the read/write head is over a symbol 1 while in state qi overwrite the 1 with b and move the tape to the right. Please note that you can define other symbols in T and you should. Consider representing two unary numbers on the tape and performing the operations in your assignment. If you include S, E in your set I you could use those symbols to recognize the start of data on the tape (S) and the end of data on the tape (E) making those symbols available to you in your state modeling. Remember that each state must fully define the operation of the DTM in that state for each symbol in I. Please note that you can define other symbols in I and you should. Consider representing two unary numbers on the tape and performing the operations in your assignment. If you include S, E in your set I you could use those symbols to recognize the start of data on the tape (S) and the end of data on the tape (E) making those symbols available to you in your state modeling. Remember that each state must fully define the operation of the DTM in that state for each symbol in T. (a) [25 Points] Implement the DTM example provided in the Course Content under Module 3. Ensure that your components as listed above are clearly identified in your variable list. The finite-state machine with the individual states, state table and five-tuple TM are shown in the above example. You should implement the following methods: i. States method, this method should have all of the operations of your TM. ii. Program line that executes the operations for each identified state, this should follow the n-tuple TM as described above for M. iii. Print method that outputs the change in tape (2 30 write the outputs to a file (b) (25 Points] Expand the implementation of the DTM in part (a) to perform additional binary operations (addition, subtraction, multiplication) at each state. You should implement the following methods that will allow for other operations: i. Addition - The tape will need to handle variable length binary inputs, e.g., tape values of 01100101 add 101 or add 101101101. Table 2: Binary Addition Rules Operation Sum Carry 3+' 0+0 0+1 1+0 1+1 ii. Subtraction - The tape will need to handle variable length binary inputs, e.g., tape values of 01100101 subtract 101 or subtract 101101101. ii. Subtraction - The tape will need to handle variable length binary inputs, e.g., tape values of 01100101 subtract 101 or subtract 101101101. Carry Table 3: Binary Subtraction Rules Operation Sum x - x' 0-0 0-1 0 10 1-1 iii. Multiplication - The tape will need to handle variable length binary inputs, e.g., tape values of 01100101 multiply 101 or multiply 101101101. Table 4: Binary Multiplication Rules Operation Multiplication OXO 0 x1 1 x 0 1x1 1 An Example DTM Consider the following example DTM. In this DTM, the alphabet recognized is r = {0, 1, b), and the set of input symbols is 2 = {0, 1). The set of states is defined to be Q = {90,91,92, 93, 94, 9N), an the transition function is defined by the following table: 1 b 90 90(90,0,+1) (90,1,+1) 91,6,-1) 91 (92,6,-1) (93,6,-1) (9.6.-1) 22 (qy.b-1) (99.6.-1) (9.6.-1) 93699.b.-1) (9.6.-1) (9.b.-1) To see this DTM program in action, view the following animation Foundations of Watch Video After viewing the demonstration, the question now becomes, "What does the program do?" Similar to finite state automata, deterministic Turing machines are said to "accept" a string if and only if the DTM "halts" in the accepting state qy. The language accepted by the DTM (or recognized by the associated program M) is given by LM = {xe 2* | M accepts x} In the example program, M accepts (x {0,1}* the right two symbols of x are 0)
