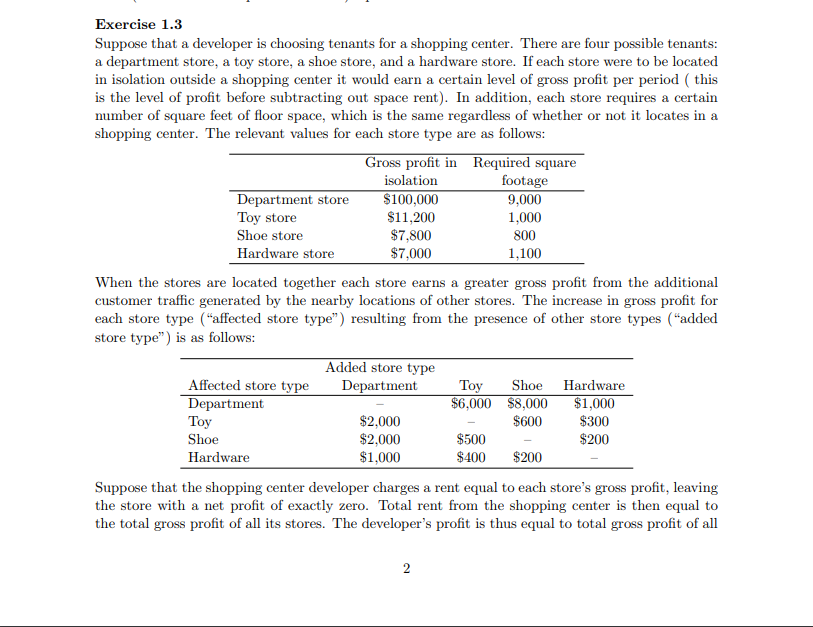
Exercise 1.3 Suppose that a developer is choosing tenants for a shopping center. There are four possible tenants: a department store, a toy store. a shoe store, and a hardware store. [teach store were to be located in isolation outside a shopping center it would earn a certain level of goes prot per period I: this is the level of prot before subtracting out space rent}. In addition, each store requires a certain number of square feet of oor space, which is the same regardless of whether or not it locates in a shopping center. The relevant values for each store type are as follows: Gross prot in Required square isolation footage Department store $100,000 $000 Toy store $11,200 1,000 Shoe store $T,800 300 Hardware store $Ty0lII 11.100 'When the stores are located together each store earns a greater gross prot from the additional customer trafc generated by the nearby locations of other stores. The increase in gross prot for each store type (\"aected store type\") resulting om the presence of other store types (\"added store type\") is as follows; Added store type Affected store type Department Toy Shoe Hardware Department $001] $3,000 $1,000 Toy $2,003 - $000 $300 Shoe $2,000 $500 $200 Hardware $L0lII $400 $200 - Suppose that the shopping center developer charges a rent equal to each store's goes prot? leaving the store with a net prot of exactly zero. Total rent from the shopping center is then equal to the total goes prot of all its stores. The developer's prot is thus equal to total goes prot of all stores in the center minus the cost of providing space). Finally, suppose that, owing to high-quality construction and the need to provide common space around the stores, the construction cost for the shopping center space is high. In particular, suppose that the cost per period per square foot of store foot space is $111]. {a} Give an intuitive explanation for the pattern of incremental prots from the presence of other stores in the second table above. {h} Suppose the developer were to construct a single-store shopping center ( a contradiction in terms, perhaps). There are four types of such centers 1: a department store alone, a toy store alone, and so on}. Using the information above, compute the developer's prot from each of these four types of centers. (c) Next compute the developer's prot om the various types of two-store shopping centers {i.e., department store plus shoe store, department store plus toy store, and so on; how many possibilities are there?) {:21} Finally, compute prots form the various types of three-store centers and from the single type of four-store center. [e] Comparing your answers from [h], {c}, and d}, identi the optimal shopping center (the one yielding the highest prot to the developer}. Explain intuitively why this particular collection of stores is optimal