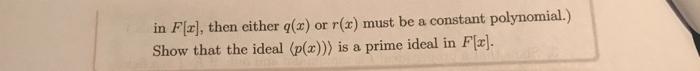
Exercise 2.133 Let R be a commutative ring. A proper ideal I of R is said to be prime if whenever ab e I for a and b in R, then either a or b must be in I. 1. Show that I is a prime ideal if and only if R/I is an integral domain. (Hint: This is just a matter of translating the definition of a prime ideal over to the ring R/I: for instance, assume that I is prime. If we have a relation [a][b]= OR/1 in R/I, then this means that ab I in R.) 2. Show that every maximal ideal is necessarily prime. 3. Show that if p is a prime integer, then the ideal (p) in Z/pZ is a prime ideal. 4. Let F be a field, and let p(x) be an irreducible polynomial in F[x]. (This means that whenever p(x) = g(x)r(r) for two polynomials in Fr], then either q(x) or r(x) must be a constant polynomial.) Show that the ideal (p(x))) is a prime ideal in F[x].