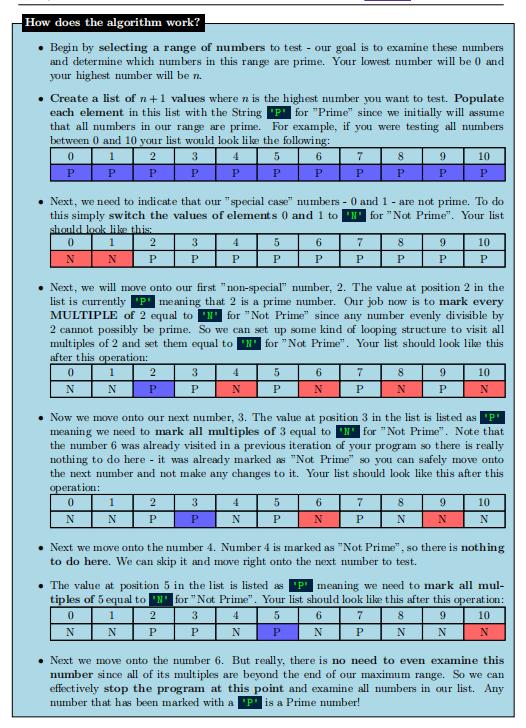
Exercise 6 - Sieve of Eratosthenes (Finding All Prime Numbers within a range) Eratosthenes of Cyrene lived approximately 275-195 BC. He was the first to accurately estimate the diameter of the earth. For several decades he served as the director and chief librarian of the famous library in Alexandria. He was highly regarded in the ancient world, but unfortunately only fragments of his writing have survived. The algorithm described for this assignment is known as the Sieve of Eratosthenes. The algorithm is designed to find all prime numbers within a given range in an interesting way - instead of testing each number to see if it is prime, it assumes that all numbers are prime. It then finds all "non prime" numbers and marks them as such. When the algorithm is finished you are left with a list of numbers along with their designation (Prime or Not Prime). How does the algorithm work? Begin by selecting a range of numbers to test - our goal is to examine these numbers and determine which numbers in this range are prime. Your lowest number will be 0 and your highest number will be n. Create a list of n+1 values where n is the highest number you want to test. Populate each element in this list with the String P for "Prime" since we initially will assume that all numbers in our range are prime. For example, if you were testing all numbers between 0 and 10 your list would look like the following: 0 1 2 3 4 5 6 7 8 9 10 P P P P P P P P P P P Next, we need to indicate that our "special case" numbers - 0 and 1 - are not prime. To do this simply switch the values of elements 0 and 1 to 'N' for "Not Prime". Your list should look like this: 0 1 2 3 4 5 6 7 8 9 10 N N P P P P P P P P P Next, we will move onto our first "non-special" number, 2. The value at position 2 in the list is currently 'P' meaning that 2 is a prime number. Our job now is to mark every MULTIPLE of 2 equal to 'N' for "Not Prime" since any number evenly divisible by 2 cannot possibly be prime. So we can set up some kind of looping structure to visit all multiples of 2 and set them equal to 'N' for "Not Prime". Your list should look like this after this operation: 0 1 2 3 4 5 6 7 8 9 10 N N P P N P N P N P N 'P' Now we move onto our next number, 3. The value at position 3 in the list is listed as | meaning we need to mark all multiples of 3 equal to 'N' for "Not Prime". Note that the number 6 was already visited in a previous iteration of your program so there is really nothing to do here it was already marked as "Not Prime" so you can safely move onto the next number and not make any changes to it. Your list should look like this after this operation: 0 1 2 3 4 5 6 7 8 9 10 N N P P N P N P N N N Next we move onto the number 4. Number 4 is marked as "Not Prime", so there is nothing to do here. We can skip it and move right onto the next number to test. The value at position 5 in the list is listed as 'P' meaning we need to mark all mul- tiples of 5 equal to "N" for "Not Prime". Your list should look like this after this operation: 0 1 2 3 4 5 6 7 8 9 10 N N P P N P N P N N N Next we move onto the number 6. But really, there is no need to even examine this number since all of its multiples are beyond the end of our maximum range. So we can effectively stop the program at this point and examine all numbers in our list. Any number that has been marked with a 'P is a Prime number! Here is your task: Ask the user for a positive integer greater than or equal to 10. Ensure the value is positive - if it is not, re-prompt the user. This number will be referred to as n. Create a list of n + 1 values... all of which are set to 'P (hint: use list repetition). This list represents the numbers 0 to n. (based on the indexes in the list) Set your "known" non-prime numbers (positions 0 and 1) to "N" for "Not Prime". Set up some kind of loop that examines all numbers from 2 through n. -If the value stored at the position you are examining is holding the value 'P' for "Prime" then you need to visit all positions that are multiples of that number and set those the value at those positions equal to N for "Not Prime". (you will probably need another loop to do this) -If the value stored at the position you are examining is holding the value "N" for "Not Prime" then you can effectively skip it and move onto the next number. When you are finished examining all numbers your program should print out all of the prime numbers that you have found in neatly aligned columns (with up to 10 prime numbers on every row). Notes on Efficiency: Efficiency is important here - here are some hints: If an item in your list has already been set to "what does this tell you about the multiples of that item's index? Do you even need to visit them? and should be replaced by True and False . Certain numbers do not need to be tested. Say you are testing all numbers between 0 and 1000 and you get to the number 800. This number cannot have any multiples less than or equal to 1000. Generalize this idea to make your program much more efficient.