Exercise Set 6.2, pages 364-366: Problems #2 (b only), #10, #15, #19, #23 (b, c, d)
Exercise Set 6.3, pages 372-374: Problems #2, #4, #16, #20, #32
Either write it out and post pic or type it out, solution needed
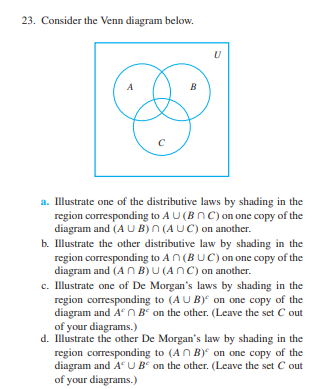
In 30-40, construct an algebraic proof for the given statement. Cite a property from Theorem 6.2.2 for every step. 32. For all sets A and B. (A - B) U(AnB) = A.For each of 1-4 find a counterexample to show that the state- H 14. For all sets A, B, and C. if AnCC BAC and ment is false. Assume all sets are subsets of a universal set U. AUCC BUC, then A C B. 1. For all sets A, B, and C. (AnB) UC = An (BUC). H 15. For all sets A, B, and C. if AnC = BAC and AUC = BUC, then A = B. 2. For all sets A and B. (AU BY = AU B. 3. For all sets A, B, and C, if A 2 B and B & C then A & C. 16. For all sets A and B, if An B = / then A x B = 1. 4. For all sets A, B, and C. if BNC C A then 17. For all sets A and B. if A C B then P(A) C S(B). (A - B)n(A - C) = 4. 18. For all sets A and B. P(AUD) C S(A)US(B). For each of 5-21 prove each statement that is true and find a H 19. For all sets A and B. P(A)US(B) C P(AUB). counterexample for each statement that is false. Assume all sets are subsets of a universal set U. 20. For all sets A and B. P(AnB) = "(A)nS(B). 5. For all sets A, B, and C. A - (B - C) = (A - B) - C. 21. For all sets A and B. "(A x B) = P(A) x P(B). 6. For all sets A and B, An (AUB) = A. 22. Write a negation for each of the following statements. Indi- cate which is true, the statement or its negation. Justify your 7. For all sets A, B, and C. answers. (A - B)n (C - B) = A - (BUC). a. V sets S, 3 a set 7 such that Sn T = 0. b. 3 a set S such that V sets T, SUT = 1. 8. For all sets A and B, if A C B then A U B = U. H 23. Let S = (a, b, c) and for each integer i = 0, 1, 2, 3, let S; 9. For all sets A. B. and C. if A CC and B CC then be the set of all subsets of S that have / clements. List the AUBCC. elements in So, 51, $2, and $3. Is (So, $1, 52, Sa] a partition of P(5)? 10. For all sets A and B. if A C B then An B* = 1. 24. Let S = (a, b, c) and let S, be the set of all subsets of $ that H 11. For all sets A, B, and C, if A C B then An (BnCy = 1. contain a, let S, be the set of all subsets of $ that contain H 12. For all sets A, B. and C, b, let S, be the set of all subsets of $ that contain c, and let So be the set whose only element is (. Is (5., Sy, S,, S,) a An(B-C) = (AnB) - (AnC). partition of (5)? 13. For all sets A, B, and C, AU(B- C) = (AUB) - (AUC).23. Consider the Venn diagram below. a. Illustrate one of the distributive laws by shading in the region corresponding to A U (8 n C) on one copy of the diagram and (A U B)n (A U C) on another. b. Illustrate the other distributive law by shading in the region corresponding to An (B U C) on one copy of the diagram and (A n B) U (An C) on another. c. Illustrate one of De Morgan's laws by shading in the region corresponding to (A U B) on one copy of the diagram and An Be on the other. (Leave the set C out of your diagrams.) d. Illustrate the other De Morgan's law by shading in the region corresponding to (An B) on one copy of the diagram and AU Be on the other. (Leave the set C out of your diagrams.)Use an element argument to prove each statement in 7-19. Assume that all sets are subsets of a universal set U. H 7. For all sets A and B, (AnBy = AUB. 8. For all sets A and B, (AnB) U (AnB') = A. H 9. For all sets A, B, and C, (A - B)U (C - B) = (A UC) - B. 10. For all sets A, B, and C. (A - D)n (C - B) = (AnC) - B. H 11. For all sets A and B, AU (An B) = A. 12. For all sets A, A UN = A. 13. For all sets A, B, and C, if A C B then AnCC BAC. 14. For all sets A, B, and C, if A C B then A UCC BUC. 15. For all sets A and B, if A C B then B C A. H 16. For all sets A, B, and C. if A C B and A C C then ACBNC. 17. For all sets A, B. and C. if A C C and B C C then AUBCC. 18. For all sets A, B, and C, A x ( B UC) = (A x B)U (A x C). 19. For all sets A, B, and C, A x (B n C) = (A x B)n (A x C).Exercise Set 6.2 1. a. To say that an element is in An (B U C) means that it is 2. The following are two proofs that for all sets A and B. in ) and in (2) A - B C A. The first is less formal, and the second is more b. To say that an element is in (An B) U C means that it is formal. Fill in the blanks. in _{1) or in (2) a. Proof: Suppose A and B are any sets. To show that c. To say that an element is in A - (8 n C) means that it A - B C A, we must show that every element in _(1) is in (1) and not in (2) is in 14) . But any element in A - B is in (3) - and not