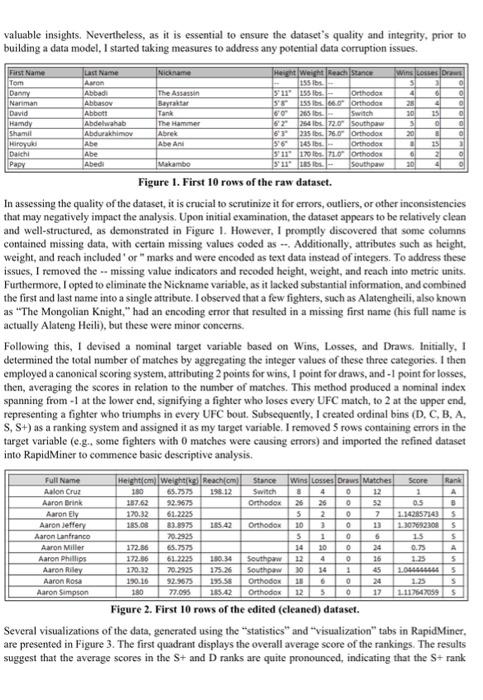
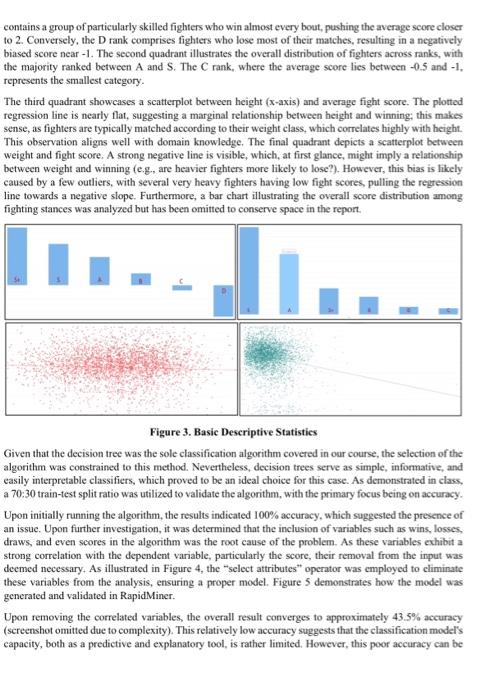
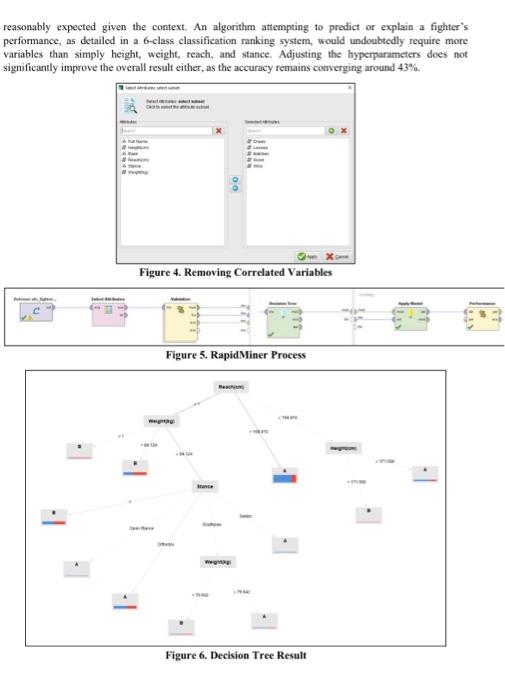
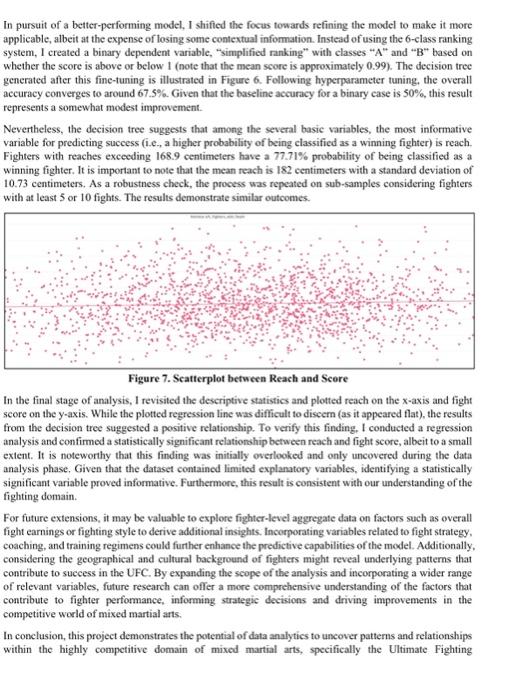
Exploring Data Analytics with Real-World Datasets The domain chosen for this project is the Ultimate Fighting Championship (UFC), a leading mixed martial arts organization that features some of the most talented fighters globally. A personal interest and bobby in combat sports drove the selection of the UFC domain, presenting a unique opportunity to explore and analyze various aspects of this competitive and fast-paced discipline. Examining data from wins, losses. draws, and other relevant factors, as well as diverse fighter attributes and performance metries, allows for a deeper understanding of the multifaceted nature of combat sports, which aligns with personal interests. The motivation for investigating the UFC domain extends beyond personal passion, as it offers the potential to apply data analytics techniques to uncover pattems and relationships among fighter characteristics, performance outcomes, and competitive dynamics. By analyzing basic fighter information, such as height, weight, and reach, alongside fight outcomes, this project aims to provide a more comprehensive understanding of the factors influencing fighter performance. The insights derived from this analysis hold significant business implications, as they can be advantageous for various stakeholders, including fighters, coaches, promoters, and sports analysts. Leveraging this knowledge can lead to more informed decision-making, refined training strategies, and improved overall competitiveness within the sport. Thus, examining the UFC domain from a data-driven perspective not only aligns with personal interests but also contributes to a greater understanding of the complex interactions within the realm of combat sports. Building upon the rationale for selecting the UFC domain and the potential insights that can be gained from the data analysis, the primary research question to be addressed in this project is: How do basic fighter characteristics, such as beight, weight, reach, and stance, influence fight outcomes, specifically in terms of wins, losses, and draws? This question aligns with the broader objective of uncovering patterns and relationships among fighter attributes, performance outcomes, and competitive dynamics within the context of mixed mantial arts. By investigating these connections, I focus to provide a more comprehensive understanding of the factors driving fighter suecess and contribute to the existing body of knowledge on the complex interactions that govern the realm of combat sports. The dataset chosen for this project is sourced from Kaggle, a reputable platform for data science and machine learning projects. The dataset, titled "UFC Data" can be found at the following link: hittps:/ /www kagglc com/datascts fatismaili/ufe-data. It contains information on fighters and events from UFC Stats, offering a rich and valuable resource for examining various aspects of mixed martial arts. The dataset comprises 3,591 records and 10 attributes, providing an extensive collection of data on UFC fighters. The attributes included in the dataset are as follows: First Name, Last Name, Nickname, Height, Weight, Reach, Stance, Wins, Losses, and Draws. These attributes are a mixture of nominal and integerbased data types, which enables a preliminary data analysis. For the classification task at hand, the target variable will be the number of wins, as it serves as a critical measure of a fighter's success and performance within the UFC. Investigating the relationship between fighter attributes and the number of wins will enable a deeper understanding of the factors that contribute to a fighter's success in the highly competitive realm of mixed martial arts. However, given that a Decision Tree classifier algorithm will be employed, which operates on nominal values, it will be necessary to transform the dependent variable into a nominal one. For instance, calcuiating the average wins fot fighters and creating a binary variable indicating whether a fighter has an above-average win rate could be a viable approach. Alternatively, generating a nominal variable that combines wins, losses, and draws might offer valuable insights. Nevertheless, as it is essential to ensure the dataset's quality and integrity, prior to building a data model, I started taking measures to address any potential data corruption issues. Figure 1. First 10 rows of the raw dataset. In assessing the quality of the dataset, it is crucial to scrutinize it for errors, outliers, or other inconsistencies that may negatively impact the analysis. Upon initial examination, the dataset appears to be relatively clean and well-structured, as demonstrated in Figure 1. However, 1 promptly discovered that some columns contained missing data, with certain missing values coded as ... Additionally, attributes such as beight, weight, and reach included ' or " marks and were encoded as text data instead of integers. To address these issues, I removed the -- missing value indicators and recoded height, weight, and reach into metric units. Furthermore, I opted to eliminate the Nickname variable, as it lacked substantial information, and combined the first and last name into a single attribute. I observed that a few fighters, such as Alatengheili, also known as "The Mongolian Knight," had an encoding error that resulted in a missing first name (his full name is actually Alateng Heili), but these were minor concerns. Following this, 1 devised a nominal target variable based on Wins, Losses, and Draws. Initially, I determined the total number of matches by aggregating the integer values of these three categories. I then employed a canonical scoring system, attributing 2 points for wins, 1 point for draws, and -1 point for losses, then, averaging the scores in relation to the number of matehes. This method produced a nominal index spanning from -1 at the lower end, signifying a fighter who loses every UFC match, to 2 at the upper end, representing a fighter who triumphs in every UFC bout. Subsequently, I created ordinal bins (D, C, B, A. S,S+ ) as a ranking system and assigned it as my target variable. I removed 5 rows containing errors in the target variable (e.g.4 some fighters with 0 matehes were causing errors) and imported the refined dataset into RapidMiner to commence basic descriptive analysis. Figure 2. First 10 rows of the edited (eleaned) dataset. Several visualizations of the data, generated using the "statistics" and "visualization" tabs in RapidMiner. are presented in Figure 3. The first quadrant displays the overall average score of the rankings. The results suggest that the average scores in the S+ and D ranks are quite pronounced, indicating that the S+ rank contains a group of particularly skilled fighters who win almost every bout, pushing the average score closer to 2. Conversely, the D rank comprises fighters who lose most of their matches, resulting in a negatively biased score near -1 . The second quadrant illustrates the overall distribution of fighters across ranks, with the majority ranked between A and S. The C rank, where the average score lies between -0.5 and -1 , represents the smallest category. The third quadrant showcases a scatterplot between height ( x-axis) and average fight score. The plotted regression line is nearly flat, suggesting a marginal relationship between height and winning; this makes sense, as fighters are typically matched according to their weight class, which correlates highly with height. This observation aligns well with domain knowledge. The final quadrant depicts a scatterplot between weight and fight score. A strong negative line is visible, which, at first glance, might imply a relationship between weight and winning (e.g., are heavier fighters more likely to lose?). However, this bias is likely caused by a few outliers, with several very heavy fighters having low fight scores, pulling the regression line towards a negative slope. Furthermore, a bar chart illustrating the overall score distribution among fighting stances was analyzed but has been omitted to conserve space in the report. Figure 3. Basic Descriptive Statistics Given that the decision tree was the sole classification algorithm covered in our course, the selection of the algorithm was constrained to this method. Nevertheless, decision trees serve as simple, informative, and easily interpretable classifiers, which proved to be an ideal choice for this case. As demonstrated in class, a 70:30 train-test split ratio was utilized to validate the algorithm, with the primary focus being on accuracy. Upon initially running the algorithm, the results indicated 100% accuracy, which suggested the presence of an issue. Upon further investigation, it was determined that the inclusion of variables such as wins, losses, draws, and even scores in the algorithm was the root cause of the problem. As these variables exhibit a strong correlation with the dependent variable, particularly the score, their removal from the input was deemed necessary. As illustrated in Figure 4, the "select attributes" operator was employed to climinate these variables from the analysis, ensuring a proper model. Figure 5 demonstrates how the model was generated and validated in RapidMiner. Upon removing the correlated variables, the overall result converges to approximately 43.5% accuracy (screenshot omitted due to complexity). This relatively low accuracy suggests that the classification model's capacity, both as a predictive and explanatory tool, is rather limited. However, this poor accuracy can be reasonably expected given the context. An algorithm attempting to predict or explain a fighter's performance, as detailed in a 6-elass classification ranking system, would undoubtedly require more variables than simply height, weight, reach, and stance. Adjusting the hyperparameters does not significantly improve the overall result either, as the accuracy remains converging around 43%. Figure 4. Removing Correlated Variables Figure 5. RapidMiner Process Figure 6. Decision Tree Result In pursuit of a better-performing model, I shified the focus towards refining the model to make it more applicable, albeit at the expense of losing some contextual information. Instead of using the 6 -class ranking system, I created a binary dependent variable, "simplified ranking" with classes " A " and " B " based on whether the score is above or below 1 (note that the mean score is approximately 0.99 ). The decision tree generated after this fine-tuning is illustrated in Figure 6. Following hyperparameter tuning, the overall accuracy converges to around 67.5%. Given that the baseline accuracy for a binary case is 50%, this result represents a somewhat modest improvement. Nevertheless, the decision tree suggests that among the several basic variables, the most informative variable for predieting success (i.e., a higher probability of being classified as a winning fighter) is reach. Fighters with reaches exceeding 168.9 centimeters have a 77.71% probability of being classified as a winning fighter. It is important to note that the mean reach is 182 centimeters with a standard deviation of 10.73 centimeters. As a robustness check, the process was repeated on sub-samples considering fighters with at least 5 or 10 fights. The results demonstrate similar outcomes. Figure 7. Seatterplot between Reach and Score In the final stage of analysis, I revisited the descriptive statistics and plotted reach on the x-axis and fight score on the y-axis. While the plotted regression line was difficult to diseern (as it appeared flat), the results from the decision tree suggested a positive relationship. To verify this finding, I conducted a regression analysis and confirmed a statistically significant relationship between reach and fight score, albeit to a small extent. It is noteworthy that this finding was initially overlooked and only uncovered during the data analysis phase, Given that the dataset contained limited explanatory variables, identifying a statistically significant variable proved informative. Furthermore, this result is consistent with our understanding of the fighting domain. For future extensions, it may be valuable to explore fighter-level aggregate data on factors such as overall fight earnings or fighting style to derive additional insights. Incorporating variables related to fight strategy, coaching, and training regimens could further enhance the predictive capabilities of the model. Additionally, considering the geographical and cultural background of fighters might reveal underlying patterns that contribute to success in the UFC. By expanding the scope of the analysis and incorporating a wider range of relevant variables, future research can offer a more comprehensive understanding of the factors that contribute to fighter performance, informing strategic decisions and driving improvements in the competitive world of mixed martial arts. In conclusion, this project demonstrates the potential of data analytics to uncover patterns and relationships within the highly competitive domain of mixed martial arts, specifically the Ultimate Fighting Championship. While the initial results indicate that basic fighter characteristics have limited predictive power, the analysis did reveal a statistically significant relationship between reach and fight score (despite the marginal coefficient). The insights derived from this project may hold practical implications for various stakcholders in the realm of combat sports, contributing to more informed decision-making and strategic development. End of Assignment Sample